casa » Sanguinamento » Calcola il volume del corpo formato dalla rotazione attorno all'asse del bue. Come trovare il volume di un corpo di rivoluzione usando un integrale

Calcola il volume del corpo formato dalla rotazione attorno all'asse del bue. Come trovare il volume di un corpo di rivoluzione usando un integrale

Sezioni: Matematica

Tipo di lezione: combinato.

Lo scopo della lezione: imparare a calcolare i volumi dei corpi di rivoluzione usando gli integrali.

Compiti:

consolidare la capacità di selezionare trapezi curvilinei da una serie di forme geometriche e praticare l'abilità di calcolare le aree dei trapezi curvilinei;
conoscere il concetto di figura volumetrica;
imparare a calcolare i volumi dei corpi di rivoluzione;
promuovere lo sviluppo del pensiero logico, il discorso matematico competente, l'accuratezza nella costruzione dei disegni;
favorire l'interesse per la materia, operare con concetti e immagini matematiche, favorire la volontà, l'indipendenza, la perseveranza nel raggiungimento del risultato finale.

Durante le lezioni

I. Momento organizzativo.

Saluto di gruppo. Comunicare gli obiettivi della lezione agli studenti.

Riflessione. melodia calma.

- La lezione di oggi vorrei iniziare con una parabola. “C'era un saggio che sapeva tutto. Una persona voleva dimostrare che il saggio non sa tutto. Stringendo la farfalla tra le mani, chiese: "Dimmi, saggio, quale farfalla ho tra le mani: viva o morta?" E lui stesso pensa: "Il vivo dirà - la ucciderò, il morto dirà - la libererò". Il saggio, pensando, rispose: "Tutto nelle tue mani". (Presentazione.Diapositiva)

“Pertanto, lavoriamo fruttuosamente oggi, acquisiamo un nuovo bagaglio di conoscenze e applichiamo le abilità e le abilità acquisite nella vita successiva e nelle attività pratiche. "Tutto nelle tue mani".

II. Ripetizione di materiale studiato in precedenza.

- Ricordiamo i punti principali del materiale studiato in precedenza. Per fare ciò, completeremo l'attività "Elimina la parola in più."(Diapositiva.)

(Lo studente va a I.D. con l'aiuto di una gomma rimuove una parola in più.)

- Destra "Differenziale". Prova a nominare le parole rimanenti con una parola generica. (Calcolo integrale.)

- Ricordiamo le principali fasi e concetti associati al calcolo integrale ..

“Gruppo matematico”.

Esercizio. Ripristina le lacune. (Lo studente esce e scrive le parole necessarie con una penna.)

- Ascolteremo in seguito un abstract sull'applicazione degli integrali.

Lavora sui quaderni.

- La formula di Newton-Leibniz è stata derivata dal fisico inglese Isaac Newton (1643-1727) e dal filosofo tedesco Gottfried Leibniz (1646-1716). E questo non sorprende, perché la matematica è la lingua parlata dalla natura stessa.

- Consideriamo come questa formula viene utilizzata nella risoluzione di compiti pratici.

Esempio 1: Calcola l'area di una forma delimitata da linee

Soluzione: costruiamo grafici di funzioni sul piano delle coordinate ... Seleziona l'area della forma da trovare.

III. Imparare nuovo materiale.

- Presta attenzione allo schermo. Cosa viene mostrato nella prima immagine? (Diapositiva) (La figura mostra una figura piatta.)

- Cosa viene mostrato nella seconda immagine? Questa cifra è piatta? (Diapositiva) (La figura mostra una figura tridimensionale.)

- Nello spazio, sulla terra e nella vita di tutti i giorni, incontriamo non solo figure piatte, ma anche tridimensionali, ma come calcolare il volume di tali corpi? Ad esempio, il volume di un pianeta, una cometa, un meteorite, ecc.

- Pensano al volume sia quando costruiscono case, sia quando versano acqua da una nave all'altra. Le regole e le tecniche per il calcolo dei volumi avrebbero dovuto sorgere, è un'altra questione quanto fossero accurate e ragionevoli.

Messaggio dello studente. (Vera Tyurina.)

L'anno 1612 fu molto fruttuoso per gli abitanti della città austriaca di Linz, dove viveva a quel tempo il famoso astronomo Johannes Kepler, soprattutto per l'uva. Le persone stavano preparando botti di vino e volevano sapere come determinarne praticamente il volume. (Diapositiva 2)

- Così, le opere considerate di Keplero gettarono le basi per un intero flusso di studi che culminò nell'ultimo quarto del XVII secolo. registrazione nelle opere di I. Newton e G.V. Calcolo differenziale e integrale di Leibniz. Da quel momento la matematica delle variabili di grandezza ha occupato un posto di primo piano nel sistema della conoscenza matematica.

- Oggi saremo impegnati in tali attività pratiche, quindi,

L'argomento della nostra lezione è "Calcolo dei volumi dei corpi di rivoluzione usando un integrale definito". (Diapositiva)

- Imparerai la definizione di un corpo di rivoluzione completando il seguente compito.

"Labirinto".

Labirinto (parola greca) significa entrare in una prigione. Labirinto - un'intricata rete di percorsi, passaggi, stanze comunicanti tra loro.

Ma la definizione "si è schiantata", ci sono suggerimenti sotto forma di frecce.

Esercizio. Trova una via d'uscita dalla confusione e scrivi la definizione.

Diapositiva. “Istruzioni sulla mappa” Calcolo dei volumi.

Utilizzando un integrale definito, si può calcolare il volume di un corpo, in particolare, un corpo di rivoluzione.

Un corpo di rivoluzione è un corpo ottenuto ruotando un trapezio curvo attorno alla sua base (Fig. 1, 2)

Il volume del corpo di rivoluzione viene calcolato utilizzando una delle formule:

1. intorno all'asse OX.

2. se la rotazione del trapezio curvo intorno all'asse del sistema operativo.

Ogni studente riceve una scheda di istruzione. L'istruttore sottolinea i punti principali.

- L'istruttore spiega la soluzione con esempi alla lavagna.

Consideriamo un estratto dalla famosa fiaba di Alexander Pushkin "Il racconto dello zar Saltan, il figlio del suo glorioso e potente eroe, il principe Gvidon Saltanovich e la bellissima principessa Lebed" (Diapositiva 4):

…..
E ha portato un messaggero ubriaco
Lo stesso giorno, l'ordine è il seguente:
“Il re ordina ai suoi boiardi,
Non perdere tempo
E la regina e la prole
Gettati di nascosto nell'abisso delle acque”.
Non c'è niente da fare: boiardi,
Dopo aver spinto per il sovrano
E la giovane regina,
Sono venuti nella sua camera da letto in mezzo alla folla.
Annunciarono la volontà del re -
Lei e suo figlio hanno una brutta sorte,
Leggi ad alta voce il decreto
E la regina alla stessa ora
Hanno messo mio figlio in una botte,
Macinato, guidato
E l'hanno fatto entrare nell'okiyan -
Questo è ciò che ha ordinato lo zar Saltan.

Quale dovrebbe essere il volume della canna per adattarsi alla regina e a suo figlio?

- Considera i seguenti compiti

1. Trova il volume del corpo ottenuto ruotando il trapezio curvo attorno all'asse delle ordinate, delimitato dalle linee: x 2 + y 2 = 64, y = -5, y = 5, x = 0.

Risposta: 1163 cm 3 .

Trova il volume di un corpo ottenuto ruotando un trapezio parabolico attorno all'asse delle ascisse y =, x = 4, y = 0.

IV. Protezione di nuovo materiale

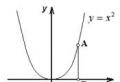
Esempio 2. Calcola il volume del corpo formato dalla rotazione del petalo attorno all'asse delle ascisse y = x2, y2 = x.

Costruiamo i grafici della funzione. y = x 2, y 2 = x... Programma y2 = x conversione nella forma sì= .

Abbiamo V = V 1 - V 2 Calcoliamo il volume di ogni funzione

- Ora, diamo un'occhiata alla torre per una stazione radio a Mosca su Shabolovka, costruita secondo il progetto di un meraviglioso ingegnere russo, l'accademico onorario V.G. Shukhov. Consiste di parti - iperboloidi di rivoluzione. Inoltre, ciascuno di essi è costituito da barre metalliche rettilinee che collegano cerchi adiacenti (Fig. 8, 9).

- Considera il problema.

Trova il volume del corpo ottenuto ruotando gli archi dell'iperbole attorno al suo asse immaginario, come mostrato in Fig. 8 dove

cucciolo. unità

Compiti di gruppo. Gli studenti tirano a sorte i compiti, disegnano i disegni su un foglio Whatman, uno dei rappresentanti del gruppo difende il lavoro.

1° gruppo.

Colpire! Colpire! Un altro colpo!
Una palla vola nel cancello - PALLA!
E questa è una palla di cocomero
Verde, rotondo, gustoso.
Guarda meglio - che palla!
È fatto dagli stessi cerchi.
Tagliare l'anguria a cerchi
E assaggiarli.

Trova il volume del corpo ottenuto ruotando la funzione attorno all'asse OX, limitato

Errore! Segnalibro non definito.

- Dimmi, per favore, dove incontriamo questa figura?

Casa. compito per 1 gruppo. CILINDRO (diapositiva) .

"Cilindro - che cos'è?" - Ho chiesto a mio padre.
Il padre rise: Un cilindro è un cappello.
Per avere un'idea corretta,
Il cilindro è, diciamo, un barattolo di latta.
Tubo del vapore - cilindro,
Anche il camino sul nostro tetto,

Tutti i tubi sono simili a un cilindro.
E ho fatto un esempio come questo -
Il mio adorato caleidoscopio
Non puoi distogliere gli occhi da lui
E sembra anche un cilindro.

- Esercizio. Compito a casa è quello di rappresentare graficamente la funzione e calcolare il volume.

2° gruppo. CONO (diapositiva).

La mamma ha detto: E ora
La mia storia riguarderà il cono.
Astrologo col cappello alto
Conta le stelle tutto l'anno.
CONO - Cappello da astrologo.
Questo è quello che è. Inteso? Questo è tutto.
La mamma stava al tavolo,
Ha versato l'olio nelle bottiglie.
- Dov'è l'imbuto? Nessun imbuto.
Aspetto. Non farti da parte.
- Mamma, non mi muovo,
Dicci di più sul cono.
- L'imbuto ha la forma di un cono di annaffiatoio.
Dai, trovamela il prima possibile.
Non sono riuscito a trovare un imbuto,
Ma la mamma ha fatto una borsa
Ho attorcigliato il cartone intorno al mio dito
E abilmente lo ha fissato con una graffetta.
L'olio sta versando, la mamma è contenta
Il cono è uscito esattamente ciò di cui avevamo bisogno.

Esercizio. Calcola il volume del corpo ottenuto mediante rotazione attorno all'asse delle ascisse

Casa. compito per il 2° gruppo. PIRAMIDE(diapositiva).

Ho visto la foto. In questa immagine
C'è una PIRAMIDE nel deserto sabbioso.
Tutto nella piramide è straordinario
C'è del mistero e del mistero in esso.
Una torre Spasskaya sulla Piazza Rossa
Familiarità sia per i bambini che per gli adulti molto bene.
Guardi la torre - di aspetto ordinario,
E cosa c'è sopra di lei? Piramide!

Esercizio. Compiti a casa per rappresentare graficamente la funzione e calcolare il volume della piramide

- Abbiamo calcolato i volumi dei vari corpi in base alla formula di base per i volumi dei corpi utilizzando un integrale.

Questa è un'altra conferma che un integrale definito ha qualche fondamento per lo studio della matematica.

- Bene, ora riposiamoci un po'.

Trova una coppia.

Sta suonando una melodia matematica del domino.

"La strada che io stesso stavo cercando non sarà mai dimenticata..."

Ricerca. Applicazione dell'integrale in economia e tecnologia.

Test per studenti forti e calcio matematico.

Simulatore matematico.

2. L'insieme di tutte le derivate di una data funzione si chiama

A) un integrale indefinito,

B) funzione,

C) differenziazione.

7. Trova il volume del corpo ottenuto ruotando un trapezio curvo attorno all'asse delle ascisse, delimitato da linee:

D/Z. Calcola i volumi dei corpi di rivoluzione.

Riflessione.

Ricezione della riflessione nella forma sincronizzare(cinque versi).

1a riga - nome dell'argomento (un sostantivo).

2a riga - descrizione dell'argomento in due parole, due aggettivi.

3a riga: descrizione dell'azione nell'ambito di questo argomento in tre parole.

4a riga - una frase di quattro parole, mostra la relazione con l'argomento (intera frase).

La quinta riga è un sinonimo che ripete l'essenza dell'argomento.

Volume.
Funzione integrale definita, integrabile.
Costruiamo, ruotiamo, calcoliamo.
Il corpo ottenuto ruotando un trapezio curvo (attorno alla sua base).
Corpo di rivoluzione (corpo geometrico solido).

Produzione (diapositiva).

Un integrale definito è una base per lo studio della matematica, che fornisce un contributo insostituibile alla risoluzione di problemi di contenuto pratico.
Il tema "Integrale" dimostra chiaramente il collegamento tra matematica e fisica, biologia, economia e tecnologia.
Lo sviluppo della scienza moderna è inconcepibile senza l'uso di un integrale. A questo proposito, è necessario iniziare a studiarlo nell'ambito dell'istruzione secondaria specializzata!

Classificazione. (Con commento.)

Il grande Omar Khayyam è un matematico, poeta, filosofo. Chiama ad essere i padroni del tuo destino. Ascoltiamo un estratto del suo lavoro:

Dirai che questa vita è un momento.
Apprezzala, trai ispirazione da lei.
Mentre lo spendi, passerà.
Non dimenticare: lei è una tua creazione.

Utilizzando un integrale definito, si può calcolare non solo area di figure piatte, ma anche i volumi dei corpi formati dalla rotazione di queste figure attorno agli assi coordinati.

Esempi di tali corpi sono mostrati nella figura seguente.

Nei compiti, abbiamo trapezi curvi che ruotano attorno a un asse Bue o intorno all'asse ahi... Per calcolare il volume di un corpo formato dalla rotazione di un trapezio curvo, abbiamo bisogno di:

il numero "pi" (3.14 ...);
un integrale definito del quadrato del "gioco" - una funzione che definisce una curva rotante (questo se la curva ruota attorno all'asse Bue );
integrale definito del quadrato "x", espresso dal "gioco" (questo se la curva ruota attorno all'asse ahi );
limiti di integrazione - un e B.

Quindi, il corpo, che è formato dalla rotazione attorno all'asse Bue trapezio curvilineo delimitato dall'alto dal grafico della funzione sì = F(X) , ha volume

Volume simile v corpo ottenuto per rotazione attorno all'asse delle ordinate ( ahi) di un trapezio curvilineo è espresso dalla formula

Quando si calcola l'area di una figura piatta, abbiamo appreso che le aree di alcune figure possono essere trovate come differenza di due integrali, in cui gli integrandi sono quelle funzioni che limitano la figura dall'alto e dal basso. La situazione è simile con alcuni corpi di rivoluzione, i cui volumi sono calcolati come differenza tra i volumi di due corpi, tali casi sono discussi negli esempi 3, 4 e 5.

Esempio 1.Bue) figure delimitate da iperbole, ascisse e rette,.

Soluzione. Il volume del corpo di rivoluzione si trova con la formula (1), in cui, e i limiti di integrazione un = 1 , B = 4 :

Esempio 2. Trova il volume di una palla di raggio R.

Soluzione. Consideriamo una palla come un corpo, ottenuto mediante rotazione attorno all'asse delle ascisse di un semicerchio di raggio R centrata nell'origine. Quindi, nella formula (1), l'integrando sarà scritto nella forma e i limiti dell'integrazione sono - R e R... Quindi,

Esempio 3. Trova il volume del corpo formato dalla rotazione attorno all'asse delle ascisse ( Bue) della figura racchiusa tra le parabole e.

Soluzione. Rappresentiamo il volume richiesto come la differenza tra i volumi dei corpi ottenuti ruotando trapezi curvilinei attorno all'asse delle ascisse ABCDE e ABFDE... Troviamo i volumi di questi corpi mediante la formula (1), in cui i limiti di integrazione sono uguali e sono le ascisse dei punti B e D intersezione di parabole. Ora possiamo trovare il volume del corpo:

Esempio 4. Calcola il volume di un toro (un toro è un corpo ottenuto ruotando un cerchio di raggio un attorno ad un asse giacente nel suo piano a distanza B dal centro del cerchio (). La forma di un toro è, ad esempio, un volante).

Soluzione. Lascia che il cerchio ruoti attorno all'asse Bue(fig. 20). Il volume di un toro può essere rappresentato come la differenza tra i volumi dei corpi ottenuti dalla rotazione di trapezi curvi ABCDE e ABLDE intorno all'asse Bue.

Equazione del cerchio LBCD ha la forma

e l'equazione della curva BCD

e l'equazione della curva BLD

Usando la differenza tra i volumi dei corpi, si ottiene per il volume del toro v espressione

Il volume di un corpo di rivoluzione può essere calcolato con la formula:

Nella formula, c'è sempre un numero davanti all'integrale. È successo così: tutto ciò che ruota nella vita è collegato a questa costante.

Come impostare i limiti di integrazione "a" e "bh", credo, sia facile da indovinare dal disegno completato.

Funzione... cos'è questa funzione? Diamo un'occhiata al disegno. Una figura piatta è delimitata in alto da un grafico a parabola. Questa è la funzione implicita nella formula.

Negli esercizi pratici, a volte una figura piatta può essere posizionata sotto l'asse. Questo non cambia nulla - l'integrando nella formula è al quadrato: quindi l'integrale è sempre non negativo , il che è abbastanza logico.

Calcoliamo il volume del corpo di rivoluzione utilizzando questa formula:

Come ho già notato, l'integrale è quasi sempre semplice, l'importante è stare attenti.

Risposta:

Nella risposta, è necessario indicare la dimensione - unità cubiche. Cioè, nel nostro corpo di rivoluzione ci sono circa 3,35 "cubi". Perché esattamente cubico? unità? Perché la formulazione più universale. Potrebbero esserci centimetri cubi, potrebbero esserci metri cubi, potrebbero esserci chilometri cubi, ecc., ecco quanti omini verdi la tua immaginazione può mettere in un disco volante.

Esempio 2

Trova il volume del corpo formato dalla rotazione attorno all'asse della figura delimitato dalle linee ,,

Questo è un esempio di soluzione fai-da-te. Soluzione completa e risposta alla fine del tutorial.

Considera due compiti più complessi che sono anche comuni nella pratica.

Esempio 3

Calcolare il volume del corpo ottenuto ruotando la cifra delimitata dalle linee attorno all'asse delle ascisse, e

Soluzione: Disegna una figura piana nel disegno, delimitata da linee ,,,, senza dimenticare che l'equazione imposta l'asse:

La figura desiderata è ombreggiata in blu. Quando lo ruoti attorno all'asse, ottieni una ciambella così surreale con quattro angoli.

Il volume del corpo di rivoluzione si calcola come differenza nei volumi del corpo.

Per prima cosa, diamo un'occhiata alla forma delineata in rosso. Quando ruota attorno all'asse, si ottiene un tronco di cono. Indichiamo il volume di questo tronco di cono passante.

Considera la forma delineata in verde. Se ruoti questa figura attorno all'asse, otterrai anche un cono troncato, solo leggermente più piccolo. Indichiamo il suo volume attraverso.

E, ovviamente, la differenza di volumi è esattamente il volume della nostra "ciambella".

Usiamo la formula standard per trovare il volume di un corpo di rivoluzione:

1) La figura tratteggiata in rosso è delimitata dall'alto da una linea retta, quindi:

2) La sagoma cerchiata in verde è delimitata dall'alto da una linea retta, quindi:

3) Il volume del corpo di rivoluzione cercato:

Risposta:

È curioso che in questo caso la soluzione possa essere verificata utilizzando la formula scolastica per il calcolo del volume di un cono troncato.

La soluzione stessa viene spesso abbreviata, qualcosa del genere:

Ora riposiamoci e parliamo di illusioni geometriche.

Le persone spesso hanno illusioni associate ai volumi, che Perelman (un altro) ha notato nel libro Geometria interessante... Guarda la figura piatta nel problema risolto: sembra essere piccola nell'area e il volume del corpo di rivoluzione è poco più di 50 unità cubiche, che sembra troppo grande. A proposito, la persona media in tutta la sua vita beve un liquido con un volume di una stanza di 18 metri quadrati, che, al contrario, sembra essere di volume troppo piccolo.

In generale, il sistema educativo in URSS era davvero il migliore. Lo stesso libro di Perelman, pubblicato nel lontano 1950, sviluppa molto bene, come diceva l'umorista, il ragionamento e insegna a cercare soluzioni originali non standard ai problemi. Recentemente ho riletto alcuni capitoli con molto interesse, lo consiglio, è disponibile anche per le discipline umanistiche. No, non c'è bisogno di sorridere che ho offerto un tempo libero, erudizione e una visione ampia nella comunicazione è una grande cosa.

Dopo la digressione lirica, è giusto risolvere il compito creativo:

Esempio 4

Calcola il volume di un corpo formato per rotazione attorno all'asse di una figura piana delimitata da linee, dove.

Questo è un esempio di soluzione fai-da-te. Si prega di notare che tutto avviene nella striscia, in altre parole, vengono effettivamente dati dei limiti di integrazione già pronti. Disegna correttamente i grafici delle funzioni trigonometriche, lascia che ti ricordi il materiale della lezione su trasformazioni geometriche di grafici : se l'argomento è divisibile per due:, i grafici vengono allungati lungo l'asse due volte. È desiderabile trovare almeno 3-4 punti dalle tabelle trigonometriche per completare più accuratamente il disegno. Soluzione completa e risposta alla fine del tutorial. A proposito, il compito può essere risolto razionalmente e non molto razionalmente.

Il volume di un corpo di rivoluzione può essere calcolato con la formula:

Nella formula, c'è sempre un numero davanti all'integrale. È successo così: tutto ciò che ruota nella vita è collegato a questa costante.

Come impostare i limiti di integrazione "a" e "bh", credo, sia facile da indovinare dal disegno completato.

Funzione... cos'è questa funzione? Diamo un'occhiata al disegno. Una figura piatta è delimitata in alto da un grafico a parabola. Questa è la funzione implicita nella formula.

Negli esercizi pratici, a volte una figura piatta può essere posizionata sotto l'asse. Questo non cambia nulla - la funzione nella formula è al quadrato: quindi il volume di un corpo di rivoluzione è sempre non negativo, il che è abbastanza logico.

Calcoliamo il volume del corpo di rivoluzione utilizzando questa formula:

Come ho già notato, l'integrale è quasi sempre semplice, l'importante è stare attenti.

Risposta:

Esempio 2

Trova il volume del corpo formato dalla rotazione attorno all'asse della figura delimitato da linee,

Questo è un esempio di soluzione fai-da-te. Soluzione completa e risposta alla fine del tutorial.

Considera due compiti più complessi che sono anche comuni nella pratica.

Esempio 3

Calcolare il volume del corpo ottenuto ruotando la cifra delimitata dalle linee attorno all'asse delle ascisse, e

Soluzione: Disegna nel disegno una figura piatta delimitata da linee,,,, senza dimenticare che l'equazione imposta l'asse:

La figura desiderata è ombreggiata in blu. Quando lo ruoti attorno all'asse, ottieni una ciambella così surreale con quattro angoli.

Il volume del corpo di rivoluzione si calcola come differenza nei volumi del corpo.

Per prima cosa, diamo un'occhiata alla forma delineata in rosso. Quando ruota attorno all'asse, si ottiene un tronco di cono. Indichiamo il volume di questo tronco di cono passante.

Considera la forma delineata in verde. Se ruoti questa figura attorno all'asse, otterrai anche un cono troncato, solo un po' più piccolo. Indichiamo il suo volume attraverso.

E, ovviamente, la differenza di volumi è esattamente il volume della nostra "ciambella".

Usiamo la formula standard per trovare il volume di un corpo di rivoluzione:

1) La figura tratteggiata in rosso è delimitata dall'alto da una linea retta, quindi:

2) La sagoma cerchiata in verde è delimitata dall'alto da una linea retta, quindi:

3) Il volume del corpo di rivoluzione cercato:

Risposta:

È curioso che in questo caso la soluzione possa essere verificata utilizzando la formula scolastica per il calcolo del volume di un cono troncato.

La soluzione stessa viene spesso abbreviata, qualcosa del genere:

Ora riposiamoci e parliamo di illusioni geometriche.

Le persone hanno spesso illusioni associate ai volumi, che Perelman (non quello) ha notato nel libro. Geometria interessante... Guarda la figura piatta nel problema risolto: sembra essere piccola nell'area e il volume del corpo di rivoluzione è poco più di 50 unità cubiche, che sembra troppo grande. A proposito, la persona media in tutta la sua vita beve un liquido con un volume di una stanza di 18 metri quadrati, che, al contrario, sembra essere di volume troppo piccolo.

In generale, il sistema educativo in URSS era davvero il migliore. Lo stesso libro di Perelman, scritto da lui nel 1950, sviluppa molto bene, come diceva l'umorista, il ragionamento e insegna a cercare soluzioni originali non standard ai problemi. Recentemente ho riletto alcuni capitoli con molto interesse, lo consiglio, è disponibile anche per le discipline umanistiche. No, non c'è bisogno di sorridere che ho offerto un tempo libero, erudizione e una visione ampia nella comunicazione è una grande cosa.

Dopo la digressione lirica, è giusto risolvere il compito creativo:

Esempio 4

Calcola il volume di un corpo formato per rotazione attorno all'asse di una figura piana delimitata da linee, dove.

Questo è un esempio di soluzione fai-da-te. Tieni presente che tutto avviene nella striscia, in altre parole, sono dati limiti di integrazione quasi preconfezionati. Prova anche a disegnare correttamente i grafici delle funzioni trigonometriche, se l'argomento è divisibile per due:, i grafici vengono allungati lungo l'asse due volte. Prova a trovare almeno 3-4 punti dalle tabelle trigonometriche ed eseguire più accuratamente il disegno. Soluzione completa e risposta alla fine del tutorial. A proposito, il compito può essere risolto razionalmente e non molto razionalmente.

Calcolo del volume di un corpo formato per rotazione
una figura piatta attorno a un asse

Il secondo paragrafo sarà ancora più interessante del primo. Anche il compito di calcolare il volume di un corpo di rivoluzione attorno all'asse delle ordinate è un ospite abbastanza frequente nei test. Lungo la strada, sarà considerato il problema di trovare l'area di una figura nel secondo modo: l'integrazione lungo l'asse, questo ti consentirà non solo di migliorare le tue abilità, ma ti insegnerà anche come trovare la soluzione più redditizia. C'è anche un senso pratico della vita in questo! Come ha ricordato con un sorriso la mia insegnante di didattica della matematica, molti laureati l'hanno ringraziata con le parole: "La tua materia ci ha aiutato molto, ora siamo manager efficaci e gestiamo il personale in modo ottimale". Cogliendo l'occasione, le esprimo anche la mia profonda gratitudine, soprattutto perché uso le conoscenze acquisite per lo scopo previsto =).

Esempio 5

Ti viene data una figura piatta delimitata da linee,,.

1) Trova l'area di una figura piatta delimitata da queste linee.
2) Trova il volume di un corpo ottenuto ruotando una figura piatta delimitata da queste linee attorno a un asse.

Attenzione! Anche se vuoi leggere solo il secondo paragrafo, prima necessariamente leggi il primo!

Soluzione: Il compito ha due parti. Cominciamo dal quadrato.

1) Eseguiamo il disegno:

È facile vedere che la funzione definisce il ramo superiore della parabola e la funzione definisce il ramo inferiore della parabola. Davanti a noi c'è una banale parabola che "sta dalla sua parte".

La cifra richiesta, la cui area deve essere trovata, è ombreggiata in blu.

Come faccio a trovare l'area di una forma? Può essere trovato nel modo "solito", che è stato discusso nella lezione Integrale definito. Come calcolare l'area di una forma... Inoltre, l'area della figura si trova come somma delle aree:
- sul segmento;
- sul segmento.

Ecco perchè:

Cosa c'è di sbagliato nella solita soluzione in questo caso? Innanzitutto, ci sono due integrali. In secondo luogo, le radici sotto gli integrali, e le radici negli integrali non sono un dono, inoltre ci si può confondere nella sostituzione dei limiti dell'integrazione. In effetti, gli integrali, ovviamente, non sono mortali, ma in pratica tutto può essere molto più triste, ho appena raccolto funzioni migliori per il compito.

C'è un modo più razionale per risolverlo: consiste nel passare alle funzioni inverse e nell'integrare lungo l'asse.

Come si passa alle funzioni inverse? In parole povere, devi esprimere "x" attraverso "gioco". Affrontiamo prima la parabola:

È abbastanza, ma assicuriamoci che la stessa funzione possa essere estratta dal ramo inferiore:

Con una linea retta, tutto è più semplice:

Ora diamo un'occhiata all'asse: per favore, inclina periodicamente la testa a destra di 90 gradi mentre spieghi (non è uno scherzo!). La forma di cui abbiamo bisogno si trova sul segmento indicato dalla linea tratteggiata rossa. In questo caso, sul segmento, la linea retta si trova sopra la parabola, il che significa che l'area della figura dovrebbe essere trovata usando la formula che ti è già familiare:. Cosa è cambiato nella formula? Solo una lettera e niente di più.

! Nota: è necessario impostare i limiti di integrazione lungo l'asse rigorosamente dal basso verso l'alto!

Trova la zona:

Sul segmento, quindi:

Fate attenzione a come ho effettuato l'integrazione, questo è il modo più razionale, e nel prossimo paragrafo del compito sarà chiaro il perché.

Per i lettori che hanno dubbi sulla correttezza dell'integrazione, troverò le derivate:

Si ottiene l'integrando originale, il che significa che l'integrazione viene eseguita correttamente.

Risposta:

2) Calcoliamo il volume del corpo formato dalla rotazione di questa figura attorno all'asse.

Ridisegnerò il disegno con un design leggermente diverso:

Quindi, la forma ombreggiata in blu ruota attorno all'asse. Il risultato è una "farfalla in bilico" che ruota attorno al proprio asse.

Per trovare il volume di un corpo di rivoluzione, integreremo lungo l'asse. Per prima cosa devi andare alle funzioni inverse. Questo è già stato fatto e dettagliato nel paragrafo precedente.

Ora incliniamo di nuovo la testa a destra e studiamo la nostra figura. Ovviamente, il volume di un corpo di rivoluzione dovrebbe essere trovato come differenza di volumi.

Ruota la forma delineata in rosso attorno all'asse, ottenendo un cono troncato. Designiamo questo volume attraverso.

Ruota la forma, cerchiata in verde, attorno all'asse e denotala attraverso il volume del corpo di rivoluzione risultante.

Il volume della nostra farfalla è uguale alla differenza di volumi.

Usiamo la formula per trovare il volume di un corpo di rivoluzione:

Qual è la differenza dalla formula del paragrafo precedente? Solo nella lettera.

Ed ecco il vantaggio dell'integrazione, di cui ho parlato di recente, è molto più facile da trovare che elevare prima l'integrando alla quarta potenza.

Risposta:

Tuttavia, una farfalla malaticcia.

Nota che se ruoti la stessa figura piatta attorno all'asse, ottieni un corpo di rotazione completamente diverso, di volume diverso, ovviamente.

Esempio 6

Ti viene data una figura piatta delimitata da linee e un asse.

1) Vai alle funzioni inverse e trova l'area di una figura piatta delimitata da queste linee integrando su una variabile.
2) Calcolare il volume di un corpo ottenuto ruotando una figura piana delimitata da queste linee attorno ad un asse.

Questo è un esempio di soluzione fai-da-te. Chi è interessato può anche trovare l'area della figura nel modo "consueto", verificando così il punto 1). Ma se, ripeto, ruoti una figura piatta attorno a un asse, otterrai un corpo di rotazione completamente diverso con un volume diverso, tra l'altro, la risposta corretta (anche per coloro a cui piace risolvere).

La soluzione completa dei due punti proposti del compito alla fine della lezione.

Oh, e non dimenticare di inclinare la testa a destra per capire i corpi della rivoluzione e all'interno dell'integrazione!

Volevo, lo era già, finire l'articolo, ma oggi hanno portato un esempio interessante solo per trovare il volume di un corpo di rivoluzione attorno all'asse delle ordinate. Appena:

Esempio 7

Calcola il volume del corpo formato dalla rotazione attorno all'asse della figura delimitato dalle curve e. Il ramo sinistro inutilizzato della parabola corrisponde alla funzione inversa - il grafico della funzione si trova sul segmento sopra l'asse;

È logico supporre che il volume del corpo di rivoluzione va cercato già come la somma dei volumi dei corpi di rivoluzione!

Usiamo la formula:

In questo caso:

Risposta:

V il problema di trovare l'area di una figura la sommatoria delle aree viene spesso utilizzata e la sommatoria dei volumi dei corpi di rivoluzione, apparentemente, è una rarità, poiché una tale varietà è quasi uscita dal mio campo visivo. Tuttavia, è positivo che l'esempio considerato sia arrivato in modo tempestivo: siamo riusciti a tirare fuori molte cose utili.

Promozione di figure di successo!

Inoltre trovare l'area di una figura piana usando un integrale definito l'applicazione più importante del tema è calcolo del volume di un corpo di rivoluzione... Il materiale è semplice, ma il lettore deve essere preparato: bisogna saper risolvere integrali indefiniti di media complessità e applicare la formula di Newton-Leibniz in integrale definito ... Come per il problema di trovare l'area, hai bisogno di abilità di disegno sicure: questa è quasi la cosa più importante (poiché gli stessi integrali saranno spesso facili). Puoi padroneggiare una tecnica grafica competente e veloce con l'aiuto di materiale metodologico ... Ma, in effetti, ho già ripetutamente parlato dell'importanza dei disegni nella lezione. .

In generale, ci sono molte applicazioni interessanti nel calcolo integrale, usando un integrale definito puoi calcolare l'area di una figura, il volume di un corpo di rivoluzione, la lunghezza di un arco, l'area della superficie di un corpo e molto altro. Quindi sarà divertente, per favore sii ottimista!

Immagina una figura piatta sul piano delle coordinate. Ti sei presentato? ... mi chiedo chi ha presentato cosa ... =))) Abbiamo già trovato la sua area. Ma, inoltre, questa figura può anche essere ruotata e ruotata in due modi:

– intorno all'asse delle ascisse; - intorno all'asse delle ordinate.

Questo articolo coprirà entrambi i casi. Il secondo metodo di rotazione è particolarmente interessante, causa le maggiori difficoltà, ma in effetti la soluzione è praticamente la stessa della più comune rotazione attorno all'asse delle ascisse. Come bonus, tornerò a il problema di trovare l'area di una figura , e ti dirò come trovare l'area nel secondo modo: lungo l'asse. Non è nemmeno tanto un bonus in quanto il materiale si adatta bene all'argomento.

Cominciamo con il tipo di spin più popolare.

Calcolo del volume di un corpo formato ruotando una figura piana attorno a un asse

Esempio 1

Calcola il volume di un solido ottenuto ruotando una forma delimitata da linee attorno a un asse.

Soluzione: Come nel problema di trovare l'area, la soluzione inizia con il disegno di una figura piatta... Cioè, su un piano è necessario costruire una figura delimitata da linee e non dimenticare che l'equazione imposta l'asse. Come realizzare un disegno in modo più efficiente e veloce, puoi scoprirlo nelle pagine Grafici e proprietà delle funzioni elementari e Integrale definito. Come calcolare l'area di una forma ... Questo è un promemoria cinese e non mi fermo più a questo punto.

Il disegno qui è piuttosto semplice:

La figura piatta desiderata è ombreggiata in blu, è lei che ruota attorno all'asse. Il risultato della rotazione è un disco volante leggermente ovoidale che è simmetrico rispetto all'asse. In effetti, il corpo ha un nome matematico, ma il libro di riferimento è troppo pigro per essere guardato, quindi andiamo oltre.

Come calcolare il volume di un corpo di rivoluzione?

Il volume di un corpo di rivoluzione può essere calcolato con la formula:

Nella formula, c'è sempre un numero davanti all'integrale. È successo così: tutto ciò che ruota nella vita è collegato a questa costante.

Come impostare i limiti di integrazione "a" e "bh", credo, sia facile da indovinare dal disegno completato.

Funzione... cos'è questa funzione? Diamo un'occhiata al disegno. Una figura piatta è delimitata in alto da un grafico a parabola. Questa è la funzione implicita nella formula.

Calcoliamo il volume del corpo di rivoluzione utilizzando questa formula:

Come ho già notato, l'integrale è quasi sempre semplice, l'importante è stare attenti.

Risposta:

Esempio 2

Trova il volume del corpo formato dalla rotazione attorno all'asse della figura delimitato da linee,

Questo è un esempio di soluzione fai-da-te. Soluzione completa e risposta alla fine del tutorial.

Considera due compiti più complessi che sono anche comuni nella pratica.

Esempio 3

Calcolare il volume del corpo ottenuto ruotando la cifra delimitata dalle linee attorno all'asse delle ascisse, e

Soluzione: Disegna nel disegno una figura piatta delimitata da linee,,,, senza dimenticare che l'equazione imposta l'asse: