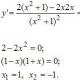Qual è la differenza di una progressione aritmetica. Come trovare la differenza di una progressione aritmetica: formule ed esempi di soluzioni

Il concetto di sequenza numerica implica che ogni numero naturale corrisponda a un valore reale. Una tale serie di numeri può essere arbitraria o avere determinate proprietà: una progressione. In quest'ultimo caso, ogni elemento successivo (membro) della sequenza può essere calcolato utilizzando quello precedente.

Una progressione aritmetica è una sequenza di valori numerici in cui i suoi membri vicini differiscono l'uno dall'altro per lo stesso numero (tutti gli elementi della serie hanno una proprietà simile, a partire dal 2 °). Questo numero - la differenza tra il termine precedente e quello successivo - è costante e si chiama differenza di progressione.

Progressione delle differenze: definizione

Si consideri una sequenza costituita da j valori A = a (1), a (2), a (3), a (4) ... a (j), j appartiene all'insieme dei numeri naturali N. Secondo la sua definizione, una progressione aritmetica è una sequenza, in cui a (3) - a (2) = a (4) - a (3) = a (5) - a (4) =… = a (j) - a (j-1) = d. Il valore d è la differenza richiesta della progressione data.

d = a (j) - a (j-1).

Assegna:

• Progressione crescente, in questo caso d> 0. Esempio: 4, 8, 12, 16, 20,…
• Progressione decrescente, quindi d< 0. Пример: 18, 13, 8, 3, -2, …

Differenza di progressione e suoi elementi arbitrari

Se sono noti 2 membri arbitrari della progressione (i-esimo, k-esimo), la differenza per questa sequenza può essere stabilita in base al rapporto:

a (i) = a (k) + (i - k) * d, quindi d = (a (i) - a (k)) / (i-k).

Differenza di progressione e suo primo termine

Questa espressione aiuterà a determinare il valore sconosciuto solo nei casi in cui è noto il numero dell'elemento della sequenza.

Differenza della progressione e sua somma

La somma della progressione è la somma dei suoi membri. Per calcolare il valore totale dei suoi primi elementi j, usa la formula appropriata:

S (j) = ((a (1) + a (j)) / 2) * j, ma poiché a (j) = a (1) + d (j - 1), quindi S (j) = ((a (1) + a (1) + d (j - 1)) / 2) * j = (( 2a (1) + d (- 1)) / 2) * j.

Istruzioni

Una progressione aritmetica è una sequenza della forma a1, a1 + d, a1 + 2d ..., a1 + (n-1) d. D a passi progressioneÈ ovvio che il totale di un termine n-esimo arbitrario dell'aritmetica progressione ha la forma: An = A1 + (n-1) d. Poi conoscendo uno dei membri progressione, membro progressione e passo progressione, puoi, cioè, il numero del membro del progresso. Ovviamente sarà determinato dalla formula n = (An-A1 + d) / d.

Ora lascia che il mese sia noto progressione e un altro membro progressione- n-esimo, ma n, come nel caso precedente, ma è noto che n e m non coincidono. progressione può essere calcolato con la formula: d = (An-Am) / (n-m). Allora n = (An-Am + md) / d.

Se si conosce la somma di più elementi dell'aritmetica progressione, oltre al primo e all'ultimo, è possibile determinare anche il numero di questi elementi. progressione sarà uguale a: S = ((A1 + An) / 2) n. Allora n = 2S / (A1 + An) - chdenov progressione... Utilizzando il fatto che An = A1 + (n-1) d, questa formula può essere riscritta come: n = 2S / (2A1 + (n-1) d). Da questo si può esprimere n risolvendo un'equazione quadratica.

Una sequenza aritmetica è un tale insieme ordinato di numeri, ogni cui membro, tranne il primo, differisce dal precedente per la stessa quantità. Questo valore costante è chiamato differenza della progressione o suo passo e può essere calcolato dai membri noti della progressione aritmetica.

Istruzioni

Se dalle condizioni del problema sono noti i valori del primo e del secondo o di qualsiasi altra coppia di termini vicini, per calcolare la differenza (d), è sufficiente sottrarre il precedente dal termine successivo. Il valore risultante può essere positivo o negativo, a seconda che la progressione sia crescente. In forma generale, scrivi la soluzione per una coppia arbitraria (aᵢ e aᵢ₊₁) di membri adiacenti della progressione come segue: d = aᵢ₊₁ - aᵢ.

Per una coppia di membri di tale progressione, di cui uno è il primo (a₁), e l'altro è qualsiasi altro scelto arbitrariamente, è anche possibile comporre una formula per trovare la differenza (d). Tuttavia, in questo caso, deve essere noto il numero di sequenza (i) di un membro arbitrario selezionato della sequenza. Per calcolare la differenza, aggiungi entrambi i numeri e dividi il risultato per il numero ordinale di un termine arbitrario, ridotto di uno. In generale, scrivi questa formula come segue: d = (a₁ + aᵢ) / (i-1).

Se, oltre a un membro arbitrario della progressione aritmetica con ordinale i, è noto un altro membro con ordinale u, modificare di conseguenza la formula del passaggio precedente. In questo caso, la differenza (d) della progressione sarà la somma di questi due termini divisa per la differenza dei loro numeri ordinali: d = (aᵢ + aᵥ) / (i-v).

La formula per calcolare la differenza (d) diventerà un po' più complicata se nel problema viene fornito il valore del suo primo termine (a₁) e la somma (Sᵢ) di un dato numero (i) dei primi membri della sequenza aritmetica condizioni. Per ottenere il valore desiderato, dividere l'importo per il numero di membri che lo compongono, sottrarre il valore del primo numero della sequenza e raddoppiare il risultato. Dividi il valore risultante per il numero di membri che compongono la somma, ridotto di uno. In generale, annotare la formula per calcolare il discriminante come segue: d = 2 * (Sᵢ / i-a₁) / (i-1).

Quando si studia l'algebra in una scuola di educazione generale (classe 9), uno degli argomenti importanti è lo studio delle sequenze numeriche, che includono progressioni - geometriche e aritmetiche. In questo articolo, considereremo la progressione aritmetica e gli esempi con soluzioni.

Che cos'è una progressione aritmetica?

Per capirlo, è necessario dare una definizione della progressione considerata, nonché fornire le formule di base che verranno ulteriormente utilizzate nella risoluzione dei problemi.

Aritmetica o è un insieme di numeri razionali ordinati, ogni termine dei quali differisce dal precedente per un valore costante. Questo valore è chiamato differenza. Cioè, conoscendo qualsiasi membro della serie ordinata di numeri e la differenza, puoi ripristinare l'intera progressione aritmetica.

Facciamo un esempio. La seguente sequenza di numeri sarà una progressione aritmetica: 4, 8, 12, 16, ..., poiché la differenza in questo caso è 4 (8 - 4 = 12 - 8 = 16 - 12). Ma l'insieme dei numeri 3, 5, 8, 12, 17 non può più essere attribuito al tipo di progressione considerato, poiché la differenza per esso non è un valore costante (5 - 3 ≠ 8 - 5 ≠ 12 - 8 ≠ 17 - 12).

Formule importanti

Diamo ora le formule di base che saranno necessarie per risolvere i problemi usando una progressione aritmetica. Indichiamo con a n l'ennesimo termine della successione, dove n è un intero. La differenza è indicata dalla lettera latina d. Allora valgono le seguenti espressioni:

1. Per determinare il valore dell'ennesimo termine, è adatta la formula: a n = (n-1) * d + a 1.
2. Per determinare la somma dei primi n termini: S n = (a n + a 1) * n / 2.

Per comprendere eventuali esempi di progressione aritmetica con soluzione al grado 9, è sufficiente ricordare queste due formule, poiché eventuali problemi del tipo in esame si basano sul loro utilizzo. Dovresti anche ricordare che la differenza di progressione è determinata dalla formula: d = a n - a n-1.

Esempio n. 1: trovare un membro sconosciuto

Diamo un semplice esempio di progressione aritmetica e formule che devono essere utilizzate per risolvere.

Sia data la sequenza 10, 8, 6, 4, ..., è necessario trovare cinque termini in essa.

Dalla dichiarazione del problema segue già che i primi 4 termini sono noti. Il quinto può essere definito in due modi:

1. Calcoliamo prima la differenza. Abbiamo: d = 8 - 10 = -2. Allo stesso modo, si potrebbero prendere altri due membri in piedi uno accanto all'altro. Ad esempio, d = 4 - 6 = -2. Poiché si sa che d = a n - a n-1, allora d = a 5 - a 4, da cui si ottiene: a 5 = a 4 + d. Sostituire i valori noti: a 5 = 4 + (-2) = 2.
2. Il secondo metodo richiede anche di conoscere la differenza della progressione considerata, quindi devi prima determinarla come mostrato sopra (d = -2). Sapendo che il primo termine a 1 = 10, usiamo la formula per n numero della sequenza. Abbiamo: a n = (n - 1) * d + a 1 = (n - 1) * (-2) + 10 = 12 - 2 * n. Sostituendo n = 5 nell'ultima espressione, otteniamo: a 5 = 12-2 * 5 = 2.

Come puoi vedere, entrambi i metodi di soluzione hanno portato allo stesso risultato. Nota che in questo esempio, la differenza d della progressione è negativa. Tali successioni sono dette decrescenti, poiché ogni termine successivo è minore del precedente.

Esempio n. 2: Differenza di progressione

Ora complichiamo un po' il compito, daremo un esempio di come trovare la differenza di una progressione aritmetica.

È noto che in alcune progressioni algebriche il 1° termine è uguale a 6 e il 7° termine è uguale a 18. È necessario trovare la differenza e riportare questa sequenza al 7° termine.

Usiamo la formula per determinare il termine sconosciuto: a n = (n - 1) * d + a 1. Sostituiamo in esso i dati noti della condizione, cioè i numeri a 1 e a 7, abbiamo: 18 = 6 + 6 * d. Da questa espressione puoi facilmente calcolare la differenza: d = (18 - 6) / 6 = 2. Abbiamo quindi risposto alla prima parte del problema.

Per ripristinare una sequenza fino a 7 termini, dovresti usare la definizione di progressione algebrica, cioè a 2 = a 1 + d, a 3 = a 2 + d, e così via. Di conseguenza, ripristiniamo l'intera sequenza: a 1 = 6, a 2 = 6 + 2 = 8, a 3 = 8 + 2 = 10, a 4 = 10 + 2 = 12, a 5 = 12 + 2 = 14 , un 6 = 14 + 2 = 16, un 7 = 18.

Esempio n. 3: fare una progressione

Complichiamo ancora di più la condizione del problema. Ora è necessario rispondere alla domanda su come trovare la progressione aritmetica. Puoi dare il seguente esempio: dati due numeri, ad esempio - 4 e 5. È necessario fare una progressione algebrica in modo che altri tre termini si adattino tra questi.

Prima di iniziare a risolvere questo problema, è necessario capire quale posto occuperanno i numeri dati nella progressione futura. Poiché ci saranno altri tre termini tra di loro, quindi a 1 = -4 e a 5 = 5. Stabilito questo, passiamo al problema, che è simile al precedente. Di nuovo, per l'ennesimo termine, usiamo la formula, otteniamo: a 5 = a 1 + 4 * d. Da dove: d = (a 5 - a 1) / 4 = (5 - (-4)) / 4 = 2,25. Qui non abbiamo ricevuto un valore intero della differenza, ma è un numero razionale, quindi le formule per la progressione algebrica rimangono le stesse.

Ora aggiungi la differenza trovata a 1 e ripristina i membri mancanti della progressione. Otteniamo: a 1 = - 4, a 2 = - 4 + 2,25 = - 1,75, a 3 = -1,75 + 2,25 = 0,5, a 4 = 0,5 + 2,25 = 2,75, a 5 = 2,75 + 2,25 = 5, che coincidono con la condizione del problema.

Esempio n. 4: il primo termine della progressione

Continuiamo a fornire esempi di progressione aritmetica con una soluzione. In tutti i problemi precedenti era noto il primo numero della progressione algebrica. Consideriamo ora un problema di tipo diverso: siano dati due numeri, dove a 15 = 50 e a 43 = 37. Occorre trovare il numero da cui inizia questa sequenza.

Le formule finora utilizzate presuppongono la conoscenza di a 1 e d. Non si sa nulla di questi numeri nella dichiarazione del problema. Tuttavia, scriviamo espressioni per ciascun membro su cui ci sono informazioni: a 15 = a 1 + 14 * d e a 43 = a 1 + 42 * d. Ha ricevuto due equazioni, in cui 2 incognite (a 1 e d). Ciò significa che il problema si riduce alla risoluzione di un sistema di equazioni lineari.

Il modo più semplice per risolvere questo sistema è esprimere un 1 in ogni equazione e quindi confrontare le espressioni risultanti. La prima equazione: a 1 = a 15 - 14 * d = 50 - 14 * d; seconda equazione: a 1 = a 43 - 42 * d = 37 - 42 * d. Uguagliando queste espressioni, otteniamo: 50 - 14 * d = 37 - 42 * d, da cui la differenza d = (37 - 50) / (42 - 14) = - 0,464 (vengono fornite solo 3 cifre decimali).

Sapendo d, puoi usare una qualsiasi delle 2 espressioni sopra per un 1. Ad esempio, il primo: a 1 = 50 - 14 * d = 50 - 14 * (- 0,464) = 56,496.

Se hai dubbi sul risultato, puoi verificarlo, ad esempio, determinare il termine 43 della progressione, che è specificato nella condizione. Otteniamo: a 43 = a 1 + 42 * d = 56,496 + 42 * (- 0,464) = 37,008. Un piccolo errore è dovuto al fatto che i calcoli hanno utilizzato l'arrotondamento al millesimo.

Esempio n. 5: importo

Vediamo ora alcuni esempi con soluzioni per la somma di una progressione aritmetica.

Sia data una progressione numerica della forma seguente: 1, 2, 3, 4, ...,. Come si calcola la somma di questi 100 numeri?

Grazie allo sviluppo della tecnologia informatica, è possibile risolvere questo problema, ovvero sommare tutti i numeri in sequenza, cosa che il computer farà non appena una persona preme il tasto Invio. Tuttavia, il problema può essere risolto nella mente, se prestiamo attenzione che la serie di numeri presentata è una progressione algebrica e la sua differenza è 1. Applicando la formula per la somma, otteniamo: S n = n * (a 1 + an) / 2 = 100 * (1 + 100) / 2 = 5050.

È curioso notare che questo problema si chiama "gaussiano", perché all'inizio del XVIII secolo il famoso tedesco, che aveva ancora solo 10 anni, riuscì a risolverlo nella sua testa in pochi secondi. Il ragazzo non conosceva la formula per la somma di una progressione algebrica, ma notò che se sommi a coppie i numeri ai lati della sequenza, ottieni sempre un risultato, cioè 1 + 100 = 2 + 99 = 3 + 98 = ..., e poiché di questi importi sarà esattamente 50 (100/2), quindi per ottenere la risposta corretta, è sufficiente moltiplicare 50 per 101.

Esempio n. 6: somma dei membri da n a m

Un altro tipico esempio di somma di una progressione aritmetica è il seguente: data una serie di numeri: 3, 7, 11, 15, ..., bisogna trovare quanto sarà uguale alla somma dei suoi membri da 8 a 14.

Il problema si risolve in due modi. Il primo consiste nel trovare termini sconosciuti da 8 a 14, e poi la loro sommatoria sequenziale. Poiché ci sono pochi termini, questo metodo non è abbastanza laborioso. Tuttavia, si propone di risolvere questo problema con il secondo metodo, che è più universale.

L'idea è di ottenere una formula per la somma della progressione algebrica tra i termini m ed n, dove n> m sono numeri interi. Scriviamo due espressioni per la somma per entrambi i casi:

1. S m = m * (un m + un 1) / 2.
2. S n = n * (un n + un 1) / 2.

Poiché n> m, è ovvio che la somma 2 include la prima. L'ultima conclusione significa che se prendiamo la differenza tra queste somme e aggiungiamo ad essa il termine a m (nel caso di prendere la differenza, viene sottratta dalla somma S n), allora otteniamo la risposta necessaria al problema. Abbiamo: S mn = S n - S m + am = n * (a 1 + an) / 2 - m * (a 1 + am) / 2 + am = a 1 * (n - m) / 2 + an * n / 2 + mattina * (1- m / 2). In questa espressione è necessario sostituire le formule a n e a m. Allora otteniamo: S mn = a 1 * (n - m) / 2 + n * (a 1 + (n - 1) * d) / 2 + (a 1 + (m - 1) * d) * (1 - m / 2) = a 1 * (n - m + 1) + d * n * (n - 1) / 2 + d * (3 * m - m 2 - 2) / 2.

La formula risultante è alquanto macchinosa; tuttavia, la somma di S mn dipende solo da n, m, a 1 e d. Nel nostro caso a 1 = 3, d = 4, n = 14, m = 8. Sostituendo questi numeri, otteniamo: S mn = 301.

Come si può vedere dalle soluzioni date, tutti i problemi si basano sulla conoscenza dell'espressione per l'ennesimo termine e della formula per la somma dell'insieme dei primi termini. Prima di procedere con la soluzione di uno qualsiasi di questi problemi, si consiglia di leggere attentamente la condizione, comprendere chiaramente cosa è necessario trovare e solo successivamente procedere alla soluzione.

Un altro consiglio è quello di cercare la semplicità, ovvero se puoi rispondere a una domanda senza utilizzare calcoli matematici complessi, allora devi fare proprio questo, poiché in questo caso la probabilità di commettere un errore è inferiore. Ad esempio, in un esempio di progressione aritmetica con soluzione n. 6, ci si potrebbe fermare alla formula S mn = n * (a 1 + an) / 2 - m * (a 1 + am) / 2 + am, e break il problema generale in attività secondarie separate (in questo caso, trovare prima i membri an e am).

In caso di dubbi sul risultato ottenuto, si consiglia di verificarlo, come è stato fatto in alcuni degli esempi riportati. Abbiamo capito come trovare la progressione aritmetica. Se lo capisci, non è così difficile.

Sì, sì: la progressione aritmetica non è un giocattolo per te :)

Bene, amici, se state leggendo questo testo, l'evidenza interna mi dice che non sapete ancora cos'è una progressione aritmetica, ma in realtà (no, così: SOOOOO!) Volete saperlo. Pertanto, non ti tormenterò con lunghe presentazioni e mi metterò subito al lavoro.

Cominciamo con un paio di esempi. Considera diversi insiemi di numeri:

• 1; 2; 3; 4; ...
• 15; 20; 25; 30; ...
• $ \ sqrt (2); \ 2 \ sqrt (2); \ 3 \ sqrt (2); ... $

Cosa hanno in comune tutti questi set? A prima vista, niente. Ma in realtà qualcosa c'è. Vale a dire: ogni elemento successivo differisce dal precedente per lo stesso numero.

Giudica tu stesso. Il primo set è semplicemente numeri consecutivi, ognuno successivo più del precedente. Nel secondo caso, la differenza tra i numeri adiacenti è già uguale a cinque, ma questa differenza è ancora costante. Nel terzo caso, radici in generale. Tuttavia, $ 2 \ sqrt (2) = \ sqrt (2) + \ sqrt (2) $ e $ 3 \ sqrt (2) = 2 \ sqrt (2) + \ sqrt (2) $, cioè e in questo caso, ogni elemento successivo aumenta semplicemente di $ \ sqrt (2) $ (e non aver paura che questo numero sia irrazionale).

Quindi: tutte queste sequenze sono chiamate progressioni aritmetiche. Diamo una definizione rigorosa:

Definizione. Una sequenza di numeri in cui ogni successivo differisce dal precedente esattamente della stessa quantità è chiamata progressione aritmetica. La stessa quantità di cui differiscono i numeri è chiamata differenza della progressione ed è spesso indicata dalla lettera $ d $.

Designazione: $ \ sinistra (((a) _ (n)) \ destra) $ - la progressione stessa, $ d $ - la sua differenza.

E solo un paio di osservazioni importanti. Prima, solo ordinato sequenza di numeri: possono essere letti rigorosamente nell'ordine in cui sono scritti - e nient'altro. Non è possibile riorganizzare o scambiare i numeri.

In secondo luogo, la sequenza stessa può essere finita o infinita. Ad esempio, l'insieme (1; 2; 3) è ovviamente una progressione aritmetica finita. Ma se scrivi qualcosa nello spirito (1; 2; 3; 4; ...) - questa è già una progressione infinita. I puntini di sospensione dopo i quattro, per così dire, suggeriscono che ci sono ancora parecchi numeri in corso. Infiniti, per esempio. :)

Vorrei anche notare che le progressioni stanno aumentando e diminuendo. Abbiamo già visto quelli crescenti - lo stesso insieme (1; 2; 3; 4; ...). Ed ecco alcuni esempi di progressioni decrescenti:

• 49; 41; 33; 25; 17; ...
• 17,5; 12; 6,5; 1; −4,5; −10; ...
• $ \ sqrt (5); \ \ sqrt (5) -1; \ \ sqrt (5) -2; \ \ sqrt (5) -3; ... $

Va bene, va bene: quest'ultimo esempio potrebbe sembrare eccessivamente complicato. Ma il resto, credo, ti è chiaro. Pertanto, introdurremo nuove definizioni:

Definizione. Una progressione aritmetica si chiama:

1. crescente se ogni elemento successivo è maggiore del precedente;
2. decrescente se, al contrario, ogni elemento successivo è minore del precedente.

Inoltre, ci sono le cosiddette sequenze "stazionarie": sono costituite dallo stesso numero ripetuto. Ad esempio, (3; 3; 3; ...).

Rimane solo una domanda: come distinguere una progressione crescente da una decrescente? Fortunatamente, tutto dipende dal segno del numero $ d $, ad es. progressione differenza:

1. Se $ d \ gt 0 $, allora la progressione è crescente;
2. Se $ d \ lt 0 $, allora la progressione è ovviamente decrescente;
3. Infine, c'è il caso $ d = 0 $ - in questo caso l'intera progressione è ridotta a una sequenza stazionaria di numeri identici: (1; 1; 1; 1; ...), ecc.

Proviamo a calcolare la differenza $ d $ per le tre progressioni decrescenti sopra riportate. Per fare ciò, è sufficiente prendere due elementi adiacenti qualsiasi (ad esempio il primo e il secondo) e sottrarre il numero a sinistra dal numero a destra. Apparirà così:

• 41−49=−8;
• 12−17,5=−5,5;
• $ \ sqrt (5) -1- \ sqrt (5) = - 1 $.

Come puoi vedere, in tutti e tre i casi, la differenza si è rivelata davvero negativa. E ora che abbiamo più o meno capito le definizioni, è tempo di capire come sono descritte le progressioni e quali sono le loro proprietà.

Membri della progressione e formula ricorrente

Poiché gli elementi delle nostre sequenze non possono essere scambiati, possono essere numerati:

\ [\ sinistra (((a) _ (n)) \ destra) = \ sinistra \ (((a) _ (1)), \ ((a) _ (2)), ((a) _ (3 )), ... \ Giusto \) \]

I singoli elementi di questo insieme sono chiamati membri della progressione. Sono indicati da un numero: il primo termine, il secondo termine, ecc.

Inoltre, come già sappiamo, i membri adiacenti della progressione sono legati dalla formula:

\ [((a) _ (n)) - ((a) _ (n-1)) = d \ Freccia destra ((a) _ (n)) = ((a) _ (n-1)) + d \]

In breve, per trovare il termine $ n $ esimo nella progressione, è necessario conoscere il termine $ n-1 $ esimo e la differenza $ d $. Tale formula è chiamata ricorrente, perché con il suo aiuto puoi trovare qualsiasi numero, conoscendo solo il precedente (e in effetti - tutti i precedenti). Questo è molto scomodo, quindi c'è una formula più complicata che riduce i calcoli al primo termine e alla differenza:

\ [((a) _ (n)) = ((a) _ (1)) + \ sinistra (n-1 \ destra) d \]

Sicuramente hai già incontrato questa formula. Amano darlo in tutti i tipi di libri di riferimento e reshebnik. E in qualsiasi libro di testo ragionevole di matematica, lei è una delle prime.

Tuttavia, suggerisco di esercitarci un po'.

Problema numero 1. Scrivi i primi tre termini della progressione aritmetica $ \ left (((a) _ (n)) \ right) $ se $ ((a) _ (1)) = 8, d = -5 $.

Soluzione. Quindi, conosciamo il primo termine $ ((a) _ (1)) = 8 $ e la differenza della progressione $ d = -5 $. Usiamo la formula appena data e sostituiamo $ n = 1 $, $ n = 2 $ e $ n = 3 $:

\ [\ inizio (allineamento) & ((a) _ (n)) = ((a) _ (1)) + \ sinistra (n-1 \ destra) d; \\ & ((a) _ (1)) = ((a) _ (1)) + \ sinistra (1-1 \ destra) d = ((a) _ (1)) = 8; \\ & ((a) _ (2)) = ((a) _ (1)) + \ sinistra (2-1 \ destra) d = ((a) _ (1)) + d = 8-5 = 3; \\ & ((a) _ (3)) = ((a) _ (1)) + \ sinistra (3-1 \ destra) d = ((a) _ (1)) + 2d = 8-10 = -2. \\ \ fine (allinea) \]

Risposta: (8; 3; -2)

È tutto! Nota: la nostra progressione sta diminuendo.

Naturalmente, $ n = 1 $ non avrebbe potuto essere sostituito - il primo termine ci è già noto. Tuttavia, sostituendone uno, ci siamo assicurati che la nostra formula funzionasse anche per il primo termine. In altri casi, tutto si riduceva a banali aritmetiche.

Problema numero 2. Scrivi i primi tre termini della progressione aritmetica se il suo settimo termine è -40 e il diciassettesimo termine è -50.

Soluzione. Scriviamo la condizione del problema nei soliti termini:

\ [((a) _ (7)) = - 40; \ quad ((a) _ (17)) = - 50. \]

\ [\ sinistra \ (\ inizio (allineamento) & ((a) _ (7)) = ((a) _ (1)) + 6d \\ & ((a) _ (17)) = ((a) _ (1)) + 16d \\ \ fine (allinea) \ destra. \]

\ [\ sinistra \ (\ inizio (allinea) & ((a) _ (1)) + 6d = -40 \\ & ((a) _ (1)) + 16d = -50 \\ \ fine (allinea) \ Giusto. \]

Metto il segno del sistema perché questi requisiti devono essere soddisfatti contemporaneamente. E ora nota che se sottraiamo la prima dalla seconda equazione (abbiamo il diritto di farlo, poiché abbiamo un sistema), otteniamo questo:

\ [\ inizio (allineamento) & ((a) _ (1)) + 16d- \ sinistra (((a) _ (1)) + 6d \ destra) = - 50- \ sinistra (-40 \ destra); \\ & ((a) _ (1)) + 16d - ((a) _ (1)) - 6d = -50 + 40; \\ & 10d = -10; \\ & d = -1. \\ \ fine (allinea) \]

È così facile che abbiamo trovato la differenza nella progressione! Resta da sostituire il numero trovato in una qualsiasi delle equazioni del sistema. Ad esempio, nel primo:

\ [\ inizio (matrice) ((a) _ (1)) + 6d = -40; \ quad d = -1 \\ \ Freccia giù \\ ((a) _ (1)) - 6 = -40; \\ ((a) _ (1)) = - 40 + 6 = -34. \\ \ fine (matrice) \]

Ora, conoscendo il primo termine e la differenza, resta da trovare il secondo e il terzo termine:

\ [\ inizio (allinea) & ((a) _ (2)) = ((a) _ (1)) + d = -34-1 = -35; \\ & ((a) _ (3)) = ((a) _ (1)) + 2d = -34-2 = -36. \\ \ fine (allinea) \]

Pronto! Il problema è stato risolto.

Risposta: (-34; -35; -36)

Prestare attenzione a una proprietà interessante della progressione che abbiamo scoperto: se prendiamo i termini $ n $ th e $ m $ th e li sottraiamo l'uno dall'altro, otteniamo la differenza della progressione moltiplicata per il numero $ n-m $:

\ [((a) _ (n)) - ((a) _ (m)) = d \ cdot \ sinistra (n-m \ destra) \]

Una proprietà semplice, ma molto utile che dovresti assolutamente conoscere: con il suo aiuto, puoi accelerare significativamente la soluzione di molti problemi nelle progressioni. Ecco un primo esempio:

Problema numero 3. Il quinto termine della progressione aritmetica è 8.4 e il suo decimo termine è 14.4. Trova il quindicesimo termine di questa progressione.

Soluzione. Poiché $ ((a) _ (5)) = 8,4 $, $ ((a) _ (10)) = 14,4 $, e devi trovare $ ((a) _ (15)) $, allora notiamo quanto segue :

\ [\ inizio (allineamento) & ((a) _ (15)) - ((a) _ (10)) = 5d; \\ & ((a) _ (10)) - ((a) _ (5)) = 5d. \\ \ fine (allinea) \]

Ma per la condizione $ ((a) _ (10)) - ((a) _ (5)) = 14,4-8,4 = $ 6, quindi $ 5d = $ 6, da cui si ha:

\ [\ inizio (allineamento) & ((a) _ (15)) - 14,4 = 6; \\ & ((a) _ (15)) = 6 + 14,4 = 20,4. \\ \ fine (allinea) \]

Risposta: 20,4

È tutto! Non abbiamo avuto bisogno di comporre alcuni sistemi di equazioni e calcolare il primo termine e la differenza: tutto è stato risolto in un paio di righe.

Ora consideriamo un altro tipo di compiti: trovare membri negativi e positivi della progressione. Non è un segreto che se la progressione aumenta, mentre il primo termine è negativo, prima o poi appariranno termini positivi. E al contrario: i membri della progressione decrescente prima o poi diventeranno negativi.

Allo stesso tempo, è tutt'altro che sempre possibile tentare questo momento "a testa alta", attraversando in sequenza gli elementi. Spesso i problemi sono progettati in modo tale che senza conoscere le formule, i calcoli richiederebbero diversi fogli: ci addormenteremmo semplicemente mentre trovavamo la risposta. Pertanto, cercheremo di risolvere questi problemi in modo più rapido.

Problema numero 4. Quanti termini negativi ci sono nella progressione aritmetica -38,5; -35.8; ...?

Soluzione. Quindi, $ ((a) _ (1)) = - 38,5 $, $ ((a) _ (2)) = - 35,8 $, da dove troviamo immediatamente la differenza:

Nota che la differenza è positiva, quindi la progressione aumenta. Il primo termine è negativo, quindi a un certo punto ci imbatteremo davvero in numeri positivi. L'unica domanda è quando accadrà.

Proviamo a scoprire: per quanto tempo (cioè fino a quale numero naturale $ n $) si conserva la negatività dei termini:

\ [\ begin (align) & ((a) _ (n)) \ lt 0 \ Rightarrow ((a) _ (1)) + \ left (n-1 \ right) d \ lt 0; \\ & -38.5+ \ left (n-1 \ right) \ cdot 2.7 \ lt 0; \ quad \ left | \ punto 10 \ destra. \\ & -385 + 27 \ cdot \ sinistra (n-1 \ destra) \ lt 0; \\ & -385 + 27n-27 \ lt 0; \\ & 27n \ lt 412; \\ & n \ lt 15 \ frac (7) (27) \ Freccia destra ((n) _ (\ max)) = 15. \\ \ fine (allinea) \]

L'ultima riga richiede un chiarimento. Quindi, sappiamo che $ n \ lt 15 \ frac (7) (27) $. D'altra parte, saremo soddisfatti solo dei valori interi del numero (inoltre: $ n \ in \ mathbb (N) $), quindi il numero più grande consentito è esattamente $ n = 15 $, e in nessun modo 16.

Problema numero 5. In progressione aritmetica $ (() _ (5)) = - 150, (() _ (6)) = - 147 $. Trova il numero del primo termine positivo di questa progressione.

Sarebbe esattamente lo stesso problema del precedente, ma non sappiamo $ ((a) _ (1)) $. Ma i termini vicini sono noti: $ ((a) _ (5)) $ e $ ((a) _ (6)) $, quindi possiamo facilmente trovare la differenza della progressione:

Inoltre, cercheremo di esprimere il quinto termine in termini del primo e la differenza secondo la formula standard:

\ [\ begin (align) & ((a) _ (n)) = ((a) _ (1)) + \ left (n-1 \ right) \ cdot d; \\ & ((a) _ (5)) = ((a) _ (1)) + 4d; \\ & -150 = ((a) _ (1)) + 4 \ cdot 3; \\ & ((a) _ (1)) = - 150-12 = -162. \\ \ fine (allinea) \]

Ora procediamo per analogia con il compito precedente. Scopriamo a che punto della nostra sequenza ci saranno numeri positivi:

\ [\ begin (align) & ((a) _ (n)) = - 162+ \ left (n-1 \ right) \ cdot 3 \ gt 0; \\ & -162 + 3n-3 \ gt 0; \\ & 3n \ gt165; \\ & n \ gt 55 \ Freccia destra ((n) _ (\ min)) = 56. \\ \ fine (allinea) \]

La soluzione intera più piccola di questa disuguaglianza è 56.

Nota: nell'ultima attività, tutto è stato ridotto a una rigida disuguaglianza, quindi l'opzione $ n = 55 $ non ci andrà bene.

Ora che abbiamo imparato a risolvere problemi semplici, passiamo a quelli più complessi. Ma prima, studiamo un'altra proprietà molto utile delle progressioni aritmetiche, che ci farà risparmiare molto tempo e celle disuguali in futuro. :)

Media aritmetica e rientri uguali

Consideriamo più membri consecutivi della progressione aritmetica crescente $ \ left (((a) _ (n)) \ right) $. Proviamo a segnarli sulla linea dei numeri:

Membri di una progressione aritmetica su una retta numerica

Ho notato specificamente termini arbitrari $ ((a) _ (n-3)), ..., ((a) _ (n + 3)) $, non qualsiasi $ ((a) _ (1)) , \ ( (a) _ (2)), \ ((a) _ (3)) $, ecc. Perché la regola, di cui ora parlerò, funziona allo stesso modo per tutti i "segmenti".

E la regola è molto semplice. Ricordiamo la formula di ricorrenza e scriviamola per tutti i membri contrassegnati:

\ [\ inizio (allineamento) & ((a) _ (n-2)) = ((a) _ (n-3)) + d; \\ & ((a) _ (n-1)) = ((a) _ (n-2)) + d; \\ & ((a) _ (n)) = ((a) _ (n-1)) + d; \\ & ((a) _ (n + 1)) = ((a) _ (n)) + d; \\ & ((a) _ (n + 2)) = ((a) _ (n + 1)) + d; \\ \ fine (allinea) \]

Tuttavia, queste uguaglianze possono essere riscritte in modo diverso:

\ [\ inizio (allineamento) & ((a) _ (n-1)) = ((a) _ (n)) - d; \\ & ((a) _ (n-2)) = ((a) _ (n)) - 2d; \\ & ((a) _ (n-3)) = ((a) _ (n)) - 3d; \\ & ((a) _ (n + 1)) = ((a) _ (n)) + d; \\ & ((a) _ (n + 2)) = ((a) _ (n)) + 2d; \\ & ((a) _ (n + 3)) = ((a) _ (n)) + 3d; \\ \ fine (allinea) \]

Bene, e allora? E il fatto che i termini $ ((a) _ (n-1)) $ e $ ((a) _ (n + 1)) $ si trovino alla stessa distanza da $ ((a) _ (n)) $ . E questa distanza è uguale a $ d $. Lo stesso si può dire dei membri $ ((a) _ (n-2)) $ e $ ((a) _ (n + 2)) $ - vengono rimossi anche da $ ((a) _ (n) ) $ la stessa distanza pari a $ 2d $. Puoi continuare all'infinito, ma il significato è ben illustrato dall'immagine.

I membri della progressione si trovano alla stessa distanza dal centro

Cosa significa questo per noi? Ciò significa che puoi trovare $ ((a) _ (n)) $ se i numeri vicini sono noti:

\ [((a) _ (n)) = \ frac (((a) _ (n-1)) + ((a) _ (n + 1))) (2) \]

Abbiamo ottenuto un'affermazione eccellente: ogni membro della progressione aritmetica è uguale alla media aritmetica dei termini vicini! Inoltre: possiamo deviare dai nostri $ ((a) _ (n)) $ sinistra e destra non un passo, ma $ k $ passi - e comunque la formula sarà corretta:

\ [((a) _ (n)) = \ frac (((a) _ (n-k)) + ((a) _ (n + k))) (2) \]

Quelli. possiamo facilmente trovare $ ((a) _ (150)) $ se sappiamo $ ((a) _ (100)) $ e $ ((a) _ (200)) $, perché $ (( a) _ (150)) = \ frac (((a) _ (100)) + ((a) _ (200))) (2) $. A prima vista, può sembrare che questo fatto non ci dia nulla di utile. Tuttavia, in pratica, molti problemi sono appositamente "affilati" per l'uso della media aritmetica. Guarda:

Problema numero 6. Trova tutti i valori di $ x $ per i quali i numeri $ -6 ((x) ^ (2)) $, $ x + 1 $ e $ 14 + 4 ((x) ^ (2)) $ sono membri consecutivi della progressione aritmetica (in ordine).

Soluzione. Poiché i numeri indicati sono membri della progressione, la condizione della media aritmetica è soddisfatta per loro: l'elemento centrale $ x + 1 $ può essere espresso in termini di elementi adiacenti:

\ [\ begin (allinea) & x + 1 = \ frac (-6 ((x) ^ (2)) + 14 + 4 ((x) ^ (2))) (2); \\ & x + 1 = \ frac (14-2 ((x) ^ (2))) (2); \\ & x + 1 = 7 - ((x) ^ (2)); \\ & ((x) ^ (2)) + x-6 = 0. \\ \ fine (allinea) \]

Il risultato è una classica equazione quadratica. Le sue radici: $ x = 2 $ e $ x = -3 $ - queste sono le risposte.

Risposta: -3; 2.

Problema numero 7. Trova i valori $$ per i quali i numeri $ -1; 4-3; (() ^ (2)) + 1 $ formano una progressione aritmetica (nell'ordine mostrato).

Soluzione. Di nuovo, esprimiamo il termine medio in termini di media aritmetica dei termini vicini:

\ [\ begin (allinea) & 4x-3 = \ frac (x-1 + ((x) ^ (2)) + 1) (2); \\ & 4x-3 = \ frac (((x) ^ (2)) + x) (2); \ quad \ left | \ punto 2 \ destra .; \\ & 8x-6 = ((x) ^ (2)) + x; \\ & ((x) ^ (2)) - 7x + 6 = 0. \\ \ fine (allinea) \]

Ancora l'equazione quadratica. E ancora ci sono due radici: $ x = 6 $ e $ x = 1 $.

Risposta 1; 6.

Se nel processo di risoluzione di un problema ti vengono fuori dei numeri brutali, o non sei completamente sicuro della correttezza delle risposte trovate, allora esiste una tecnica meravigliosa che ti consente di verificare: abbiamo risolto correttamente il problema?

Ad esempio, nel problema n.6 abbiamo ricevuto le risposte -3 e 2. Come verificare che queste risposte siano corrette? Colleghiamoli e vediamo cosa succede. Ti ricordo che abbiamo tre numeri ($ -6 (() ^ (2)) $, $ + 1 $ e $ 14 + 4 (() ^ (2)) $), che devono formare una progressione aritmetica. Sostituisci $ x = -3 $:

\ [\ inizio (allineamento) & x = -3 \ Freccia destra \\ & -6 ((x) ^ (2)) = - 54; \\ & x + 1 = -2; \\ & 14 + 4 ((x) ^ (2)) = 50. \ fine (allinea) \]

Numeri ricevuti -54; -2; 50, che differiscono per 52, è senza dubbio una progressione aritmetica. La stessa cosa accade per $ x = 2 $:

\ [\ inizio (allineamento) & x = 2 \ Freccia destra \\ & -6 ((x) ^ (2)) = - 24; \\ & x + 1 = 3; \\ & 14 + 4 ((x) ^ (2)) = 30. \ fine (allinea) \]

Di nuovo una progressione, ma con una differenza di 27. Quindi, il problema è risolto correttamente. Chi è interessato può verificare da solo il secondo problema, ma dico subito: tutto è corretto anche lì.

In generale, durante la risoluzione degli ultimi problemi, ci siamo imbattuti in un altro fatto interessante, che deve essere ricordato:

Se tre numeri sono tali che il secondo è la media aritmetica del primo e dell'ultimo, allora questi numeri formano una progressione aritmetica.

In futuro, comprendere questa affermazione ci consentirà di "costruire" letteralmente le progressioni necessarie, in base alle condizioni del problema. Ma prima di addentrarci in tale "costruzione", occorre prestare attenzione ad un altro fatto, che segue direttamente da quanto già considerato.

Raggruppamento e somma di elementi

Torniamo di nuovo all'asse dei numeri. Notiamo lì diversi membri della progressione, tra i quali, forse. ci sono molti altri membri:

La linea dei numeri ha 6 elementi contrassegnati

Proviamo ad esprimere "coda sinistra" in termini di $ ((a) _ (n)) $ e $ d $ e "coda destra" in termini di $ ((a) _ (k)) $ e $ d $ . È molto semplice:

\ [\ inizio (allinea) & ((a) _ (n + 1)) = ((a) _ (n)) + d; \\ & ((a) _ (n + 2)) = ((a) _ (n)) + 2d; \\ & ((a) _ (k-1)) = ((a) _ (k)) - d; \\ & ((a) _ (k-2)) = ((a) _ (k)) - 2d. \\ \ fine (allinea) \]

Ora, nota che le seguenti somme sono uguali:

\ [\ inizio (allinea) & ((a) _ (n)) + ((a) _ (k)) = S; \\ & ((a) _ (n + 1)) + ((a) _ (k-1)) = ((a) _ (n)) + d + ((a) _ (k)) - d = S; \\ & ((a) _ (n + 2)) + ((a) _ (k-2)) = ((a) _ (n)) + 2d + ((a) _ (k)) - 2d = s. \ fine (allinea) \]

In parole povere, se consideriamo come inizio due elementi della progressione, che in totale sono uguali a qualche $ S $ numero, e quindi iniziamo a camminare da questi elementi in direzioni opposte (l'uno verso l'altro o viceversa per allontanarci) , poi anche le somme degli elementi in cui ci imbatteremo saranno uguali$ S $. Questo può essere rappresentato graficamente più chiaramente:

Un rientro uguale dà importi uguali

Comprendere questo fatto ci consentirà di risolvere problemi di un livello di complessità fondamentalmente più elevato rispetto a quelli che abbiamo considerato sopra. Ad esempio, tale:

Problema numero 8. Determina la differenza della progressione aritmetica in cui il primo termine è 66 e il prodotto del secondo e del dodicesimo termine è il più piccolo possibile.

Soluzione. Scriviamo tutto quello che sappiamo:

\ [\ inizio (allineamento) & ((a) _ (1)) = 66; \\ & d =? \\ & ((a) _ (2)) \ cdot ((a) _ (12)) = \ min. \ fine (allinea) \]

Quindi, non conosciamo la differenza della progressione $ d $. In realtà, l'intera soluzione sarà costruita attorno alla differenza, poiché il prodotto $ ((a) _ (2)) \ cdot ((a) _ (12)) $ può essere riscritto come segue:

\ [\ inizio (allinea) & ((a) _ (2)) = ((a) _ (1)) + d = 66 + d; \\ & ((a) _ (12)) = ((a) _ (1)) + 11d = 66 + 11d; \\ & ((a) _ (2)) \ cdot ((a) _ (12)) = \ sinistra (66 + d \ destra) \ cdot \ sinistra (66 + 11d \ destra) = \\ & = 11 \cdot\sinistra (d+66\destra)\cdot\sinistra (d+6\destra). \ fine (allinea) \]

Per quelli nel serbatoio: ho tolto il fattore comune di 11 dalla seconda parentesi. Quindi, il prodotto cercato è una funzione quadratica rispetto alla variabile $ d $. Pertanto, considera la funzione $ f \ sinistra (d \ destra) = 11 \ sinistra (d + 66 \ destra) \ sinistra (d + 6 \ destra) $ - il suo grafico sarà una parabola con rami verso l'alto, poiché se espandiamo le parentesi, otteniamo:

\ [\ inizio (allineamento) & f \ sinistra (d \ destra) = 11 \ sinistra (((d) ^ (2)) + 66d + 6d + 66 \ cdot 6 \ destra) = \\ & = 11 (( d) ^ (2)) + 11 \ cdot 72d + 11 \ cdot 66 \ cdot 6 \ fine (allinea) \]

Come puoi vedere, il coefficiente al termine principale è 11 - questo è un numero positivo, quindi abbiamo davvero a che fare con una parabola con rami verso l'alto:

grafico della funzione quadratica - parabola

Nota: questa parabola prende il suo valore minimo al suo vertice con l'ascissa $ ((d) _ (0)) $. Certo, possiamo calcolare questa ascissa secondo lo schema standard (c'è anche la formula $ ((d) _ (0)) = (- b) / (2a) \; $), ma sarebbe molto più ragionevole notare che il vertice desiderato giace sull'asse di simmetria della parabola, quindi il punto $ ((d) _ (0)) $ è equidistante dalle radici dell'equazione $ f \ sinistra (d \ destra) = 0 $:

\ [\ inizio (allineamento) & f \ sinistra (d \ destra) = 0; \\ & 11 \ cdot \ sinistra (d + 66 \ destra) \ cdot \ sinistra (d + 6 \ destra) = 0; \\ & ((d) _ (1)) = - 66; \ quad ((d) _ (2)) = - 6. \\ \ fine (allinea) \]

Ecco perché non avevo fretta di aprire le parentesi: nella forma originale, le radici erano molto, molto facili da trovare. Pertanto, l'ascissa è uguale alla media aritmetica dei numeri −66 e −6:

\ [((d) _ (0)) = \ frac (-66-6) (2) = - 36 \]

Cosa ci dà il numero scoperto? Con esso, il prodotto richiesto assume il valore più piccolo (a proposito, non abbiamo contato $ ((y) _ (\ min)) $ - non ne abbiamo bisogno). Allo stesso tempo, questo numero è la differenza tra la progressione originale, ad es. abbiamo trovato la risposta. :)

Risposta: −36

Problema numero 9. Inserisci tre numeri tra i numeri $ - \ frac (1) (2) $ e $ - \ frac (1) (6) $ in modo che insieme ai numeri dati formino una progressione aritmetica.

Soluzione. Fondamentalmente, dobbiamo creare una sequenza di cinque numeri, con il primo e l'ultimo numero già noti. Indichiamo i numeri mancanti con le variabili $ x $, $ y $ e $ z $:

\ [\ sinistra (((a) _ (n)) \ destra) = \ sinistra \ (- \ frac (1) (2); x; y; z; - \ frac (1) (6) \ destra \ ) \]

Nota che il numero $ y $ è il "centro" della nostra sequenza - è equidistante sia dai numeri $ x $ e $ z $, sia dai numeri $ - \ frac (1) (2) $ e $ - \ frac (1) ( 6) $. E se al momento non possiamo ottenere $ y $ dai numeri $ x $ e $ z $, allora la situazione è diversa con le estremità della progressione. Ricordando la media aritmetica:

Ora, conoscendo $ y $, troveremo i numeri rimanenti. Nota che $ x $ si trova tra i numeri $ - \ frac (1) (2) $ e $ y = - \ frac (1) (3) $ appena trovati. Ecco perchè

Ragionando allo stesso modo, troviamo il numero rimanente:

Pronto! Abbiamo trovato tutti e tre i numeri. Scriviamoli nella risposta nell'ordine in cui devono essere inseriti tra i numeri originali.

Risposta: $ - \ frac (5) (12); \ - \ frac (1) (3); \ - \ frac (1) (4) $

Problema numero 10. Inserisci più numeri tra i numeri 2 e 42, che insieme a questi numeri formano una progressione aritmetica, se sai che la somma del primo, secondo e ultimo dei numeri inseriti è 56.

Soluzione. Un compito ancora più difficile, che però si risolve secondo lo stesso schema dei precedenti - attraverso la media aritmetica. Il problema è che non sappiamo esattamente quanti numeri inserire. Pertanto, per chiarezza, supponiamo che dopo aver inserito tutto ci saranno esattamente $ n $ numeri, e il primo di essi è 2 e l'ultimo è 42. In questo caso, la progressione aritmetica desiderata può essere rappresentata come:

\ [\ sinistra (((a) _ (n)) \ destra) = \ sinistra \ (2; ((a) _ (2)); ((a) _ (3)); ...; (( a) _ (n-1)); 42 \ destra \) \]

\ [((a) _ (2)) + ((a) _ (3)) + ((a) _ (n-1)) = 56 \]

Si noti, tuttavia, che i numeri $ ((a) _ (2)) $ e $ ((a) _ (n-1)) $ sono ottenuti dai numeri 2 e 42 ai bordi di un passo l'uno verso l'altro, cioè... al centro della sequenza. Ciò significa che

\ [((a) _ (2)) + ((a) _ (n-1)) = 2 + 42 = 44 \]

Ma allora l'espressione scritta sopra può essere riscritta come segue:

\ [\ begin (allinea) & ((a) _ (2)) + ((a) _ (3)) + ((a) _ (n-1)) = 56; \\ & \ sinistra (((a) _ (2)) + ((a) _ (n-1)) \ destra) + ((a) _ (3)) = 56; \\ & 44 + ((a) _ (3)) = 56; \\ & ((a) _ (3)) = 56-44 = 12. \\ \ fine (allinea) \]

Conoscendo $ ((a) _ (3)) $ e $ ((a) _ (1)) $, possiamo facilmente trovare la differenza della progressione:

\ [\ inizio (allinea) & ((a) _ (3)) - ((a) _ (1)) = 12 - 2 = 10; \\ & ((a) _ (3)) - ((a) _ (1)) = \ sinistra (3-1 \ destra) \ cdot d = 2d; \\ & 2d = 10 \ Freccia destra d = 5. \\ \ fine (allinea) \]

Resta solo da trovare il resto dei membri:

\ [\ inizio (allineamento) & ((a) _ (1)) = 2; \\ & ((a) _ (2)) = 2 + 5 = 7; \\ & ((a) _ (3)) = 12; \\ & ((a) _ (4)) = 2 + 3 \ cdot 5 = 17; \\ & ((a) _ (5)) = 2 + 4 \ cdot 5 = 22; \\ & ((a) _ (6)) = 2 + 5 \ cdot 5 = 27; \\ & ((a) _ (7)) = 2 + 6 \ cdot 5 = 32; \\ & ((a) _ (8)) = 2 + 7 \ cdot 5 = 37; \\ & ((a) _ (9)) = 2 + 8 \ cdot 5 = 42; \\ \ fine (allinea) \]

Pertanto, già al 9 ° passaggio arriveremo all'estremità sinistra della sequenza: il numero 42. In totale, è stato necessario inserire solo 7 numeri: 7; 12; 17; 22; 27; 32; 37.

Risposta: 7; 12; 17; 22; 27; 32; 37

Problemi di parole con le progressioni

In conclusione, vorrei prendere in considerazione un paio di compiti relativamente semplici. Bene, quanto è semplice: per la maggior parte degli studenti che studiano matematica a scuola e non hanno letto quanto scritto sopra, questi compiti possono sembrare una lattina. Tuttavia, sono proprio questi problemi che si incontrano nell'OGE e nell'USE in matematica, quindi ti consiglio di familiarizzare con loro.

Problema numero 11. La brigata ha prodotto 62 parti a gennaio e in ogni mese successivo ha prodotto 14 parti in più rispetto al precedente. Quante parti ha realizzato la squadra a novembre?

Soluzione. Ovviamente il numero di parti, programmato per mese, rappresenterà una progressione aritmetica crescente. Inoltre:

\ [\ begin (allinea) & ((a) _ (1)) = 62; \ quad d = 14; \\ & ((a) _ (n)) = 62+ \ sinistra (n-1 \ destra) \ cdot 14. \\ \ fine (allinea) \]

Novembre è l'undicesimo mese dell'anno, quindi dobbiamo trovare $ ((a) _ (11)) $:

\ [((a) _ (11)) = 62 + 10 \ cdot 14 = 202 \]

Di conseguenza, a novembre verranno prodotti 202 pezzi.

Problema numero 12. Il laboratorio di legatoria ha rilegato 216 libri a gennaio e ogni mese successivo ha rilegato 4 libri in più rispetto al precedente. Quanti libri ha rilegato il workshop a dicembre?

Soluzione. Lo stesso:

$ \ begin (allinea) & ((a) _ (1)) = 216; \ quad d = 4; \\ & ((a) _ (n)) = 216+ \ sinistra (n-1 \ destra) \ cdot 4. \\ \ fine (allinea) $

Dicembre è l'ultimo, 12° mese dell'anno, quindi stiamo cercando $ ((a) _ (12)) $:

\ [((a) _ (12)) = 216 + 11 \ cdot 4 = 260 \]

Questa è la risposta: 260 libri saranno rilegati a dicembre.

Bene, se hai letto fino a qui, mi affretto a congratularmi con te: hai completato con successo il "Corso per giovani combattenti" in progressioni aritmetiche. Puoi tranquillamente procedere alla lezione successiva, dove studieremo la formula per la somma di una progressione, nonché le conseguenze importanti e molto utili da essa.

L'argomento "progressione aritmetica" è studiato nel corso generale di algebra nelle scuole del 9° anno. Questo argomento è importante per ulteriori approfondimenti sulla matematica delle serie di numeri. In questo articolo, faremo conoscenza con la progressione aritmetica, la sua differenza, nonché con i problemi tipici che gli scolari possono affrontare.

Il concetto di progressione algebrica

Una progressione numerica è una sequenza di numeri in cui ogni elemento successivo può essere ottenuto dal precedente applicando qualche legge matematica. Esistono due semplici tipi di progressione: geometrica e aritmetica, detta anche algebrica. Soffermiamoci su di esso in modo più dettagliato.

Immaginiamo un numero razionale, denotiamolo con il simbolo a1, dove l'indice indica il suo numero ordinale nella serie considerata. Aggiungiamo un altro numero ad a1, denotiamolo con d. Quindi il secondo elemento della serie può essere riflesso come segue: a2 = a1 + d. Ora aggiungiamo di nuovo d, otteniamo: a3 = a2 + d. Continuando questa operazione matematica, puoi ottenere tutta una serie di numeri, che chiameremo progressione aritmetica.

Come si può capire da quanto sopra, per trovare l'n-esimo elemento di questa sequenza, è necessario utilizzare la formula: an = a1 + (n-1) * d. Infatti, sostituendo n = 1 nell'espressione, otteniamo a1 = a1, se n = 2, allora la formula implica: a2 = a1 + 1 * d, e così via.

Ad esempio, se la differenza della progressione aritmetica è 5 e a1 = 1, allora ciò significa che la serie numerica del tipo in esame ha la forma: 1, 6, 11, 16, 21, ... Come puoi vedi, ciascuno dei suoi membri è 5 in più del precedente.

Formule di differenza di progressione aritmetica

Dalla precedente definizione della serie di numeri in esame, ne consegue che per determinarla è necessario conoscere due numeri: a1 e d. Quest'ultimo è chiamato la differenza di questa progressione. Determina in modo univoco il comportamento dell'intera serie. Infatti, se d è positivo, allora la serie numerica aumenterà costantemente, al contrario, nel caso d negativo, ci sarà un aumento dei numeri della serie solo in valore assoluto, mentre il loro valore assoluto diminuirà all'aumentare del numero n.

Qual è la differenza tra la progressione aritmetica? Considera due formule di base che vengono utilizzate per calcolare questo valore:

d = an + 1-an, questa formula segue direttamente dalla definizione della serie di numeri in esame.

d = (-a1 + an) / (n-1), tale espressione si ottiene esprimendo d dalla formula data nel paragrafo precedente dell'articolo. Nota che questa espressione diventa ambigua (0/0) se n = 1. Ciò è dovuto al fatto che è necessaria la conoscenza di almeno 2 elementi della serie per determinarne la differenza.

Queste due formule di base servono per risolvere qualsiasi problema di trovare la differenza di progressione. Tuttavia, c'è anche un'altra formula che devi conoscere.

Somma dei primi elementi

La formula che può essere utilizzata per determinare la somma di un numero qualsiasi di membri di una progressione algebrica, secondo l'evidenza storica, fu ottenuta per la prima volta dal "principe" della matematica del XVIII secolo, Karl Gauss. Uno scienziato tedesco, quando era ancora un ragazzo delle elementari di una scuola di paese, notò che per sommare i numeri naturali in una riga da 1 a 100, bisogna prima sommare il primo elemento e l'ultimo (il valore risultante sarà uguale alla somma del penultimo e del secondo, del penultimo e del terzo elemento , e così via), e quindi questo numero deve essere moltiplicato per il numero di questi importi, cioè per 50.

La formula che riflette il risultato dichiarato per un particolare esempio può essere generalizzata a un caso arbitrario. Apparirà come: Sn = n / 2 * (an + a1). Si noti che per trovare il valore indicato non è necessaria la conoscenza della differenza d se sono noti due termini della progressione (an e a1).

Esempio 1. Determinare la differenza, conoscendo i due termini della serie a1 e an

Mostriamo come applicare le formule menzionate sopra nell'articolo. Facciamo un semplice esempio: la differenza della progressione aritmetica è sconosciuta, è necessario determinare a cosa sarà uguale se a13 = -5,6 e a1 = -12,1.

Poiché conosciamo i valori di due elementi della sequenza numerica, di cui uno è il primo numero, possiamo usare la formula n. 2 per determinare la differenza d. Abbiamo: d = (- 1 * (- 12,1) + (- 5,6)) / 12 = 0,54167. Nell'espressione, abbiamo usato il valore n = 13, poiché è noto il termine con questo particolare numero ordinale.

La differenza risultante indica che la progressione è in aumento, nonostante il fatto che i dati negli elementi di dichiarazione del problema abbiano un valore negativo. Si vede che a13> a1, sebbene | a13 |<|a1|.

Esempio n. 2. Membri positivi della progressione nell'esempio n. 1

Usiamo il risultato ottenuto nell'esempio precedente per risolvere un nuovo problema. È così formulato: da quale seriale gli elementi della progressione dell'esempio n. 1 cominceranno ad assumere valori positivi?

Come è stato mostrato, la progressione in cui a1 = -12,1 e d = 0,54167 è crescente, quindi da qualche numero i numeri inizieranno ad assumere solo valori positivi. Per determinare questo numero n è necessario risolvere una semplice disuguaglianza, che si scrive matematicamente come segue: an> 0 oppure, utilizzando l'apposita formula, riscriviamo la disuguaglianza: a1 + (n-1) * d> 0. È necessario trovare l'incognita n, esprimerla: n> -1 * a1 / d + 1. Ora resta da sostituire i valori noti della differenza e il primo termine della sequenza. Otteniamo: n> -1 * (- 12,1) / 0,54167 + 1 = 23,338 oppure n> 23,338. Poiché n può assumere solo valori interi, dalla disuguaglianza risultante segue che tutti i membri della serie che hanno un numero maggiore di 23 saranno positivi.

Controlliamo la risposta ricevuta utilizzando la formula sopra per calcolare 23 e 24 elementi di questa progressione aritmetica. Abbiamo: a23 = -12,1 + 22 * ​​0,54167 = -0,18326 (numero negativo); a24 = -12,1 + 23 * 0,54167 = 0,3584 (valore positivo). Quindi, il risultato ottenuto è corretto: partendo da n = 24, tutti i membri della serie numerica saranno maggiori di zero.

Esempio n. 3. Quanti log andranno bene?

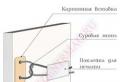
Ecco un problema interessante: durante la registrazione, si è deciso di impilare i tronchi segati uno sopra l'altro, come mostrato nella figura seguente. Quanti log possono essere impilati in questo modo, sapendo che ci saranno un totale di 10 righe?

In questo metodo di piegatura dei registri, si può notare una cosa interessante: ogni riga successiva conterrà un registro in meno della precedente, ovvero esiste una progressione algebrica, la cui differenza è d = 1. Supponendo che il numero di log in ogni riga sia un membro di questa progressione, e tenendo anche conto che a1 = 1 (solo un log starà in cima), troviamo il numero a10. Abbiamo: a10 = 1 + 1 * (10-1) = 10. Cioè, nella decima riga, che giace a terra, ci saranno 10 registri.

La somma totale di questa costruzione "piramidale" può essere ottenuta utilizzando la formula di Gauss. Otteniamo: S10 = 10/2 * (10 + 1) = 55 log.