casa » Donazione » Come trovare i punti minimo e massimo di una funzione: caratteristiche, metodi ed esempi. Punti critici della funzione Trovare il massimo

Come trovare i punti minimo e massimo di una funzione: caratteristiche, metodi ed esempi. Punti critici della funzione Trovare il massimo

I punti in cui la derivata è zero sono i punti estremi della funzione. Troviamo questi punti e definiamo i punti massimo e minimo.

x^2 - 5x + 6 = 0;

D = (- 5) ^ 2 - 4 * 1 * 6 = 25 - 24 = 1; D = 1;

x = (- b ± √D) / (2a);

x1 = (5 + 1) / 2 = 6/2 = 3;

x2 = (5 - 1) / 2 = 4/2 = 2.

Il punto massimo è il punto in cui la funzione cambia da crescente a decrescente e il punto minimo è il punto in cui la funzione cambia da decrescente ad crescente. La funzione aumenta in quegli intervalli in cui la sua derivata è positiva e diminuisce - dove la sua derivata è negativa.

Segna i punti 2 e 3 sulla linea dei numeri. Divideranno la linea in tre intervalli: 1) (- ; 2), 2) (2; 3), 3) (3; + ∞). Controlliamo il segno della derivata x ^ 2 - 5x + 6 su ogni intervallo.

Sugli intervalli 1 e 3, la derivata assume valori positivi e sugli intervalli 2 - negativi. Ciò significa che la funzione aumenta negli intervalli 1 e 3 e diminuisce negli intervalli 2. Vedi fig. http://bit.ly/2wfdf7o

Quindi il punto x = 2 è il punto di massimo e x = 3 è il punto di minimo.

Risposta. xmax = 2; xmin = 3.

Per trovare i punti estremi della funzione (cioè i punti minimo e massimo), è necessario:

trovare la derivata della funzione,
trova gli zeri della derivata (ovvero, eguagliala a zero e trova le radici dell'equazione),
utilizzando la linea dei numeri, determinare i segni della derivata: quando la funzione aumenta, la derivata è positiva, quando la funzione diminuisce, la derivata è negativa,
determinare i punti di minimo e massimo: se la funzione è aumentata e ad un certo punto ha iniziato a diminuire, allora questo è il punto di massimo e, se viceversa, questo è il punto di minimo.

La derivata è già nota f "(x) = x 2 - 5x + 6.

Trova gli zeri della derivata della funzione

x 2 - 5x + 6 = 0

Abbiamo un'equazione quadratica, troviamo le radici dell'equazione attraverso il discriminante.

x 2 - 5x + 6 - funzione quadratica, ramificata.

a = 1, b = -5, c = 6.

D = in 2 - 4ac = (-5) 2 - 4 * 1 * 6 = 25 - 24 = 1 (la radice quadrata è 1)

x 1 = (5 + 1) / 2 = 6/3 = 3

x 2 = (5 - 1) / 2 = 4/2 = 2

Determinazione dei segni della derivata

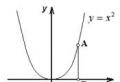
Segniamo i punti 2 e 3 sulla linea delle coordinate, disegniamo schematicamente una parabola (rami verso l'alto), segniamo segni ad ogni intervallo e usiamo le frecce per mostrare come si comporta la funzione ad ogni intervallo.

(- infinito; 2) segno più, la funzione aumenta.

(2; 3) segno meno, la funzione diminuisce.

(3; + infinito) segno più, la funzione aumenta.

Cioè, il punto 2 è un punto di massimo e il punto 3 è un punto di minimo.

Risposta: x min = 3, x max = 2.

Un semplice algoritmo per trovare gli estremi.

Trova la derivata della funzione
Uguaglia questa derivata a zero
Trova i valori della variabile dell'espressione risultante (i valori della variabile in cui la derivata viene convertita a zero)
Dividiamo la linea delle coordinate in intervalli con questi valori (allo stesso tempo, non dimenticare i punti di interruzione, che devono essere applicati anche alla linea), tutti questi punti sono chiamati punti "sospetti" per un estremo
Calcoliamo a quale di questi intervalli la derivata sarà positiva e in quale negativa. Per fare ciò, è necessario sostituire il valore dall'intervallo nella derivata.

Dei punti sospetti di un estremo, è necessario trovare esattamente. Per fare ciò, osserviamo i nostri intervalli sulla linea delle coordinate. Se, passando per un punto, il segno della derivata cambia da più a meno, allora questo punto sarà massimo, e se da meno a più, allora minimo.

Per trovare il valore più grande e più piccolo di una funzione, è necessario calcolare il valore della funzione alle estremità del segmento e ai punti estremi. Quindi scegli il valore più alto e più basso.

Consideriamo un esempio
Trova la derivata ed eguagliala a zero:

I valori risultanti delle variabili vengono applicati alla linea delle coordinate e il segno della derivata viene calcolato in ciascuno degli intervalli. Beh, per esempio, per la prima prendiamo-2 , allora la derivata sarà-0,24 , per il secondo prendiamo0 , allora la derivata sarà2 , e per il terzo prendiamo2 , allora la derivata sarà-0,24. Mettiamo i segni appropriati.

Vediamo che quando passa attraverso il punto -1, la derivata cambia segno da meno a più, cioè sarà un punto minimo, e quando passa per 1 - da più a meno, rispettivamente, questo è un punto massimo.

significato

Il più grande

significato

Meno

Punto massimo

Punto minimo

I problemi di ricerca dei punti estremi della funzione vengono risolti secondo lo schema standard in 3 passaggi.

Passo 1... Trova la derivata della funzione

Memorizzare le formule per la derivata delle funzioni elementari e le regole base di derivazione per trovare la derivata.

y ′ (x) = (x3−243x + 19) ′ = 3x2−243.

Passo 2... Trova gli zeri della derivata

Risolvi l'equazione risultante per trovare gli zeri della derivata.

3x2−243 = 0⇔x2 = 81⇔x1 = −9, x2 = 9.

Passaggio 3... Trova i punti estremi

Utilizzare il metodo della spaziatura per determinare i segni della derivata;
Al punto minimo, la derivata è uguale a zero e cambia segno da meno a più, e al punto massimo - da più a meno.

Adottiamo questo approccio per risolvere il seguente problema:

Trova il punto massimo della funzione y = x3−243x + 19.

1) Trovare la derivata: y ′ (x) = (x3−243x + 19) ′ = 3x2−243;

2) Risolvere l'equazione y ′ (x) = 0: 3x2−243 = 0⇔x2 = 81⇔x1 = −9, x2 = 9;

3) La derivata è positiva per x> 9 e x<−9 и отрицательная при −9

Come trovare il valore più grande e più piccolo di una funzione

Per risolvere il problema di trovare i valori più grande e più piccolo della funzione necessario:

Trova i punti estremi di una funzione su un segmento (intervallo).
Trova i valori alle estremità del segmento di linea e seleziona il valore più grande o più piccolo dai valori ai punti estremi e alle estremità del segmento di linea.

Aiuta in molti compiti teorema:

Se c'è un solo punto estremo sul segmento, e questo è il punto minimo, allora il valore più piccolo della funzione viene raggiunto lì. Se questo è il punto massimo, lì viene raggiunto il valore più alto.

14. Concetto e proprietà fondamentali di un integrale indefinito.

Se la funzione F(X X, e KÈ un numero, allora

In breve: la costante può essere sottratta al segno di integrale.

Se funzioni F(X) e G(X) hanno derivativi sull'intervallo X, poi

In breve: l'integrale della somma è uguale alla somma degli integrali.

Se la funzione F(X) ha una primitiva sull'intervallo X, quindi per i punti interni di questo intervallo:

In breve: la derivata dell'integrale è uguale all'integrando.

Se la funzione F(X) è continua sull'intervallo X e differenziabile nei punti interni di questo intervallo, allora:

In breve: l'integrale del differenziale di una funzione è uguale a questa funzione più la costante di integrazione.

Diamo una definizione matematica rigorosa concetti integrali indefiniti.

Un'espressione del genere si chiama integrale della funzione f(x) , dove f(x) - l'integrando, che è dato (noto), dx - differenziale X , con il simbolo è sempre presente dx .

Definizione. Integrale indefinito chiamata la funzione Fa (x) + Do contenente una costante arbitraria C il cui differenziale è uguale a integrando espressione f (x) dx , cioè. o La funzione è chiamata funzione antiderivata... L'antiderivata della funzione è determinata entro un valore costante.

Richiama questo - funzione differenziale ed è così definito:

Il compito di trovare integrale indefinitoè trovare una tale funzione, derivato che è uguale all'integrando. Questa funzione è determinata fino a una costante, poiché la derivata di una costante è uguale a zero.

Ad esempio, si sa che, poi si scopre che , ecco una costante arbitraria.

Trovare un compito integrale indefinito from functions non è così semplice e facile come sembra a prima vista. In molti casi, ci deve essere abilità nel lavorare con integrali indefiniti, ci deve essere esperienza che viene con la pratica e con la costante soluzione di esempi per integrali indefiniti. Vale la pena considerare il fatto che integrali indefiniti alcune funzioni (ce ne sono molte) non sono prese nelle funzioni elementari.

15. Tavola degli integrali indefiniti di base.

Formule di base

16. L'integrale definito come limite della somma integrale. Significato geometrico e fisico dell'integrale.

Sia definita la funzione y = ƒ (x) sul segmento [a; gruppo musicale< b. Выполним следующие действия.

1. Con l'aiuto dei punti x 0 = a, x 1, x 2, ..., x n = B (x 0

2. In ogni segmento parziale, i = 1,2, ..., n, scegli un punto arbitrario con i є e calcola il valore della funzione in esso, cioè il valore ƒ (con i).

3. Moltiplicare il valore trovato della funzione ƒ (con i) per la lunghezza ∆x i = x i -x i-1 del corrispondente segmento parziale: ƒ (con i) ∆x i.

4. Componiamo la somma S n di tutti questi prodotti:

La somma della forma (35.1) è detta somma integrale della funzione y = ƒ (x) sull'intervallo [a; B]. Sia λ la lunghezza del segmento parziale più grande: λ = max ∆x i (i = 1,2, ..., n).

5. Troviamo il limite della somma integrale (35.1) come n → ∞ in modo che λ → 0.

Se, in questo caso, la somma integrale S n ha un limite I, che non dipende dal metodo di partizione del segmento [a; b] a segmenti parziali, o dalla scelta dei punti in essi, allora il numero I si dice integrale definito della funzione y = ƒ (x) sul segmento [a; b] ed è indicato così

I numeri aeb sono chiamati, rispettivamente, i limiti inferiore e superiore di integrazione, (x) - l'integrando, ƒ (x) dx - l'integrando, x - la variabile di integrazione, il segmento [a; b] - area (segmento) di integrazione.

La funzione y = ƒ (x), per cui sul segmento [a; b] esiste un integrale definito detto integrabile su questo intervallo.

Formuliamo ora un teorema sull'esistenza di un integrale definito.

Teorema 35.1 (Cauchy). Se la funzione y = ƒ (x) è continua sul segmento [a; b], allora l'integrale definito

Si noti che la continuità di una funzione è una condizione sufficiente per la sua integrabilità. Tuttavia, un integrale definito può esistere anche per alcune funzioni discontinue, in particolare per qualsiasi funzione limitata su un intervallo e avente un numero finito di punti di discontinuità su di esso.

Indichiamo alcune proprietà dell'integrale definito che seguono direttamente dalla sua definizione (35.2).

1. L'integrale definito è indipendente dalla designazione della variabile di integrazione:

Ciò deriva dal fatto che la somma integrale (35.1), e quindi il suo limite (35.2), non dipendono da quale lettera denota l'argomento di questa funzione.

2. Un integrale definito con gli stessi limiti di integrazione è uguale a zero:

3. Per ogni numero reale c.

17. Formula di Newton-Leibniz. Proprietà fondamentali di un integrale definito.

Lascia che la funzione y = f (x) continuo sul segmento e F (x)è una delle antiderivate della funzione su questo segmento, allora Formula di Newton-Leibniz: .

La formula di Newton-Leibniz si chiama la formula base del calcolo integrale.

Per dimostrare la formula di Newton-Leibniz, abbiamo bisogno del concetto di integrale con limite superiore variabile.

Se la funzione y = f (x) continuo sul segmento , allora per l'argomento l'integrale della forma è una funzione del limite superiore. Indichiamo questa funzione , e questa funzione è continua e l'uguaglianza .

Si annota infatti l'incremento della funzione corrispondente all'incremento dell'argomento e si usa la quinta proprietà dell'integrale definito e la conseguenza della decima proprietà:

dove .

Riscriviamo questa uguaglianza come ... Se ricordiamo la definizione della derivata di una funzione e andiamo al limite a, allora otteniamo. Cioè, è una delle antiderivate della funzione y = f (x) sul segmento ... Quindi, l'insieme di tutte le derivate F (x) può essere scritto come , dove INSIEME AÈ una costante arbitraria.

calcoliamo Fa) usando la prima proprietà dell'integrale definito: , quindi, . Useremo questo risultato per il calcolo F (b): , questo è ... Questa uguaglianza dà la formula dimostrata di Newton-Leibniz .

L'incremento della funzione è solitamente indicato come ... Usando questa notazione, la formula di Newton-Leibniz assume la forma .

Per applicare la formula di Newton-Leibniz basta conoscere una delle antiderivate y = F (x) funzione integranda y = f (x) sul segmento e calcolare l'incremento di questa antiderivata su questo segmento. Nell'articolo vengono analizzate le modalità di integrazione delle principali modalità di ricerca dell'antiderivata. Ecco alcuni esempi di calcolo di integrali definiti utilizzando la formula di Newton-Leibniz per chiarimenti.

Esempio.

Calcola il valore dell'integrale definito usando la formula di Newton-Leibniz.

Soluzione.

Per cominciare, nota che l'integrando è continuo sul segmento , quindi, è integrabile su di esso. (Abbiamo parlato di funzioni integrabili nella sezione sulle funzioni per le quali esiste un integrale definito).

Dalla tabella degli integrali indefiniti si vede che per una funzione l'insieme delle derivate per tutti i valori reali dell'argomento (e quindi per) si scrive come ... Prendi l'antiderivato per C = 0: .

Ora resta da usare la formula di Newton-Leibniz per calcolare un integrale definito: .

18. Applicazioni geometriche di un integrale definito.

APPLICAZIONI GEOMETRICHE DI UN CERTO INTEGRALE

Rettangolare S.K.	Funzione, data parametricamente	Polyarnaya S.K.
Calcolo delle aree delle figure planari

Calcolo della lunghezza dell'arco di una curva piana

Calcolo della superficie di rivoluzione

Calcolo del volume corporeo

Calcolo del volume di un corpo dalle aree note di sezioni parallele:

Il volume del corpo di rotazione:; ...

Esempio 1... Trova l'area di una figura delimitata da una curva y = sinx, linee rette

Soluzione: Trova l'area della figura:

Esempio 2... Calcola l'area di una forma delimitata da linee

Soluzione: Troviamo le ascisse dei punti di intersezione dei grafici di queste funzioni. Per fare ciò, risolviamo il sistema di equazioni

Da qui troviamo x1 = 0, x2 = 2,5.

19. Il concetto di controlli differenziali. Equazioni differenziali del primo ordine.

Equazione differenziale- un'equazione che collega il valore della derivata di una funzione con la funzione stessa, i valori della variabile indipendente, i numeri (parametri). L'ordine delle derivate incluse nell'equazione può essere diverso (formalmente, non è limitato da nulla). Derivate, funzioni, variabili indipendenti e parametri possono entrare nell'equazione in varie combinazioni, oppure tutte, tranne almeno una derivata, possono essere del tutto assenti. Non tutte le equazioni che contengono derivate di una funzione sconosciuta sono equazioni differenziali. Per esempio, non è un'equazione differenziale.

Equazioni differenziali parziali(PDE) sono equazioni contenenti funzioni incognite di più variabili e le loro derivate parziali. La forma generale di tali equazioni può essere rappresentata come:

dove sono le variabili indipendenti, ed è la funzione di queste variabili. L'ordine delle equazioni differenziali alle derivate parziali può essere determinato nello stesso modo delle equazioni differenziali ordinarie. Un'altra importante classificazione delle equazioni alle derivate parziali è la loro suddivisione in equazioni di tipo ellittico, parabolico e iperbolico, soprattutto per le equazioni del secondo ordine.

Sia le equazioni differenziali ordinarie che le equazioni differenziali alle derivate parziali possono essere suddivise in lineare e non lineare... Un'equazione differenziale è lineare se la funzione incognita e le sue derivate entrano nell'equazione solo al primo grado (e non vengono moltiplicate tra loro). Per tali equazioni, le soluzioni formano un sottospazio affine dello spazio delle funzioni. La teoria della DE lineare è sviluppata molto più in profondità della teoria delle equazioni non lineari. Vista generale di un'equazione differenziale lineare n-esimo ordine:

dove p io(X) sono funzioni note della variabile indipendente, dette coefficienti dell'equazione. Funzione R(X) sul lato destro si chiama membro gratuito(l'unico termine indipendente dalla funzione sconosciuta) Un'importante classe speciale di equazioni lineari sono le equazioni differenziali lineari con coefficienti costanti.

Una sottoclasse di equazioni lineari sono omogeneo equazioni differenziali - equazioni che non contengono un termine libero: R(X) = 0. Per equazioni differenziali omogenee, il principio di sovrapposizione è soddisfatto: una combinazione lineare di soluzioni particolari di tale equazione sarà anche la sua soluzione. Tutte le altre equazioni differenziali lineari sono chiamate eterogeneo equazioni differenziali.

Nel caso generale, le equazioni differenziali non lineari non hanno sviluppato metodi di soluzione, ad eccezione di alcune classi particolari. In alcuni casi (usando certe approssimazioni) possono essere ridotti a quelli lineari. Ad esempio, l'equazione lineare di un oscillatore armonico può essere considerato come un'approssimazione dell'equazione non lineare di un pendolo matematico nel caso di piccole ampiezze, quando sì peccato sì.

· - equazione differenziale omogenea del secondo ordine a coefficienti costanti. Una soluzione è una famiglia di funzioni, dove e sono costanti arbitrarie, che per una soluzione specifica sono determinate da condizioni iniziali specificate separatamente. Questa equazione, in particolare, descrive il moto di un oscillatore armonico con frequenza ciclica 3.

La seconda legge di Newton può essere scritta sotto forma di un'equazione differenziale dove m- massa corporea, X- la sua coordinata, F(X, T) è la forza che agisce sul corpo con la coordinata X al momento T... La sua soluzione è la traiettoria del corpo sotto l'azione della forza specificata.

· L'equazione differenziale di Bessel è una normale equazione lineare omogenea del secondo ordine a coefficienti variabili: le sue soluzioni sono le funzioni di Bessel.

Un esempio di un'equazione differenziale ordinaria non lineare non uniforme del 1° ordine:

Nel prossimo gruppo di esempi, la funzione sconosciuta tu dipende da due variabili X e T o X e sì.

Equazione alle derivate parziali lineari omogenea del primo ordine:

Equazione d'onda unidimensionale - un'equazione differenziale parziale lineare omogenea del tipo iperbolico del secondo ordine con coefficienti costanti, descrive la vibrazione della corda, se - la deflessione della corda in un punto con la coordinata X al momento T e il parametro un imposta le proprietà della stringa:

L'equazione di Laplace nello spazio bidimensionale è un'equazione differenziale parziale lineare omogenea del secondo ordine di tipo ellittico a coefficienti costanti, che si pone in molti problemi fisici di meccanica, conduzione del calore, elettrostatica, idraulica:

L'equazione di Korteweg - de Vries, un'equazione differenziale parziale non lineare del terzo ordine che descrive le onde non lineari stazionarie, inclusi i solitoni:

20. Equazioni differenziali con applicabile separabile. Equazioni lineari e metodo di Bernoulli.

Un'equazione differenziale lineare del primo ordine è un'equazione lineare rispetto a una funzione sconosciuta e alla sua derivata. Ha la forma

La funzione e lo studio delle sue caratteristiche occupa uno dei capitoli chiave della matematica moderna. Il componente principale di qualsiasi funzione sono i grafici che rappresentano non solo le sue proprietà, ma anche i parametri della derivata di questa funzione. Diamo un'occhiata a questo difficile argomento. Quindi qual è il modo migliore per cercare i punti massimo e minimo di una funzione?

Funzione: definizione

Qualsiasi variabile che in qualche modo dipende dai valori di un'altra quantità può essere chiamata funzione. Ad esempio, la funzione f (x 2) è quadratica e determina i valori per l'intero insieme x. Diciamo che x = 9, quindi il valore della nostra funzione sarà pari a 9 2 = 81.

Le funzioni sono di diversi tipi: logiche, vettoriali, logaritmiche, trigonometriche, numeriche e altre. Menti eccezionali come Lacroix, Lagrange, Leibniz e Bernoulli furono impegnate nel loro studio. I loro scritti fungono da pilastro nei modi moderni di studiare le funzioni. Prima di trovare i punti di minimo, è molto importante comprendere il significato stesso della funzione e della sua derivata.

Derivato e il suo ruolo

Tutte le funzioni dipendono dai loro valori variabili, il che significa che possono cambiare il loro valore in qualsiasi momento. Sul grafico, questo sarà rappresentato come una curva che scende o sale lungo l'ordinata (questo è l'intero insieme di numeri "y" lungo la verticale del grafico). Quindi la definizione dei punti di massimo e minimo della funzione è proprio connessa a queste "fluttuazioni". Spieghiamo cos'è questa relazione.

La derivata di qualsiasi funzione viene tracciata sul grafico per studiarne le caratteristiche principali e calcolare quanto velocemente la funzione cambia (cioè cambia il suo valore in base alla variabile "x"). Nel momento in cui la funzione aumenta, aumenterà anche il grafico della sua derivata, ma in qualsiasi momento la funzione potrebbe iniziare a diminuire, e quindi il grafico della derivata diminuirà. I punti in cui la derivata va dal segno meno al più sono chiamati punti di minimo. Per sapere come trovare i punti minimi, dovresti capire meglio

Come calcolo la derivata?

Definizione e funzione implicano diversi concetti da In generale, la definizione stessa della derivata può essere espressa come segue: è il valore che mostra il tasso di variazione della funzione.

Il modo matematico di definirlo per molti studenti sembra difficile, ma in realtà è tutto molto più semplice. Hai solo bisogno di seguire il piano standard per trovare la derivata di qualsiasi funzione. Di seguito viene descritto come si può trovare il punto di minimo di una funzione senza applicare le regole di differenziazione e senza memorizzare la tavola delle derivate.

Puoi calcolare la derivata di una funzione usando un grafico. Per fare ciò, è necessario rappresentare la funzione stessa, quindi prendere un punto su di essa (punto A nella figura).Tracciare una linea verticalmente fino all'asse delle ascisse (punto x 0), e nel punto A tracciare una tangente all'asse delle ascisse. grafico della funzione. L'asse delle ascisse e la tangente formano un certo angolo a. Per calcolare il valore di quanto velocemente aumenta la funzione, è necessario calcolare la tangente di questo angolo a.
Si scopre che la tangente dell'angolo tra la tangente e la direzione dell'asse x è la derivata della funzione in una piccola sezione con il punto A. Questo metodo è considerato un modo geometrico per determinare la derivata.

Metodi di ricerca delle funzioni

Nel curriculum scolastico di matematica è possibile trovare il punto di minimo di una funzione in due modi. Abbiamo già analizzato il primo metodo utilizzando il grafico, ma come determinare il valore numerico della derivata? Per fare ciò, dovrai imparare diverse formule che descrivono le proprietà della derivata e aiutano a convertire variabili come "x" in numeri. Il seguente metodo è universale, quindi può essere applicato a quasi tutti i tipi di funzioni (sia geometriche che logaritmiche).

È necessario equiparare la funzione alla funzione derivata e quindi semplificare l'espressione utilizzando le regole di derivazione.
In alcuni casi, quando viene data una funzione in cui la variabile "x" è nel divisore, è necessario determinare l'intervallo di valori ammissibili, escludendo da esso il punto "0" (per il semplice motivo che in matematica in nessun caso puoi dividere per zero).
Successivamente, dovresti convertire la forma originale della funzione in una semplice equazione, eguagliando l'intera espressione a zero. Ad esempio, se la funzione fosse così: f (x) = 2x 3 + 38x, quindi secondo le regole di differenziazione, la sua derivata è f "(x) = 3x 2 +1. Quindi trasformiamo questa espressione in un'equazione della forma seguente: 3x 2 +1 = 0 ...
Dopo aver risolto l'equazione e aver trovato i punti "x", dovresti disegnarli sull'ascissa e determinare se la derivata in queste aree tra i punti contrassegnati è positiva o negativa. Dopo la designazione, diventerà chiaro a che punto la funzione inizia a diminuire, cioè cambia il suo segno da meno all'opposto. È in questo modo che puoi trovare sia il punto minimo che quello massimo.

Regole di differenziazione

La componente più basilare nello studio di una funzione e della sua derivata è la conoscenza delle regole di differenziazione. Solo con il loro aiuto è possibile trasformare espressioni voluminose e grandi funzioni complesse. Diamo un'occhiata a loro, ce ne sono parecchi, ma sono tutti molto semplici a causa delle proprietà naturali sia della potenza che delle funzioni logaritmiche.

La derivata di qualsiasi costante è zero (f (x) = 0). Cioè, la derivata f (x) = x 5 + x - 160 assumerà la seguente forma: f "(x) = 5x 4 +1.
Derivata della somma di due termini: (f + w) "= f" w + fw ".
Derivata di una funzione logaritmica: (log a d) "= d / ln a * d. Questa formula si applica a tutti i tipi di logaritmi.
Grado derivato: (x n) "= n * x n-1. Ad esempio, (9x 2)" = 9 * 2x = 18x.
La derivata di una funzione sinusoidale: (sin a) "= cos a. Se il sin dell'angolo a è 0,5, la sua derivata è √3 / 2.

punti estremi

Abbiamo già capito come trovare i punti di minimo, ma esiste anche un concetto di punti di massimo di una funzione. Se il minimo indica i punti in cui la funzione passa dal segno meno al più, i punti massimi sono quei punti sull'asse delle ascisse in cui la derivata della funzione cambia da più all'opposto - meno.

Puoi trovarlo con il metodo sopra descritto, ma va tenuto presente che designano quelle sezioni in cui la funzione inizia a diminuire, ovvero la derivata sarà inferiore a zero.

In matematica, è consuetudine generalizzare entrambi i concetti, sostituendoli con la frase "punti estremi". Quando l'attività chiede di determinare questi punti, significa che è necessario calcolare la derivata di questa funzione e trovare i punti minimo e massimo.

Questa sezione contiene i problemi dell'esame di matematica su argomenti relativi allo studio delle funzioni e delle loro derivate. In particolare, si tratta di trovare i valori massimo e minimo delle funzioni, dati analiticamente, cioè da una formula.

Punto massimo (minimo ) funzioni sì = F(X) chiamato valore dell'argomento x = a tale che esiste un intorno del punto un, in cui F(X) F ( un) (F(X) > F(un) ) per X ≠ un.

Massimo (minimo ) si chiama la funzione il suo significato nel punto estremo, cioè grandezza F(un) .

Così,

se il compito contiene un requisito per determinare punti estremi la risposta dovrebbe scrivere il trovato significato X ,
se hai bisogno di specificare gli estremi stessi, allora devi determinare significato sì in questi punti, sostituendoli nella formula della funzione sì = F(X) .

Per quanto riguarda i valori più grande e più piccolo della funzione su un dato intervallo , allora per una funzione continua si possono ottenere sia all'interno del segmento che alle sue estremità. Le illustrazioni grafiche per questo argomento possono essere
Se la funzione raggiunge il valore più grande (più piccolo) nel punto interno del segmento, allora questo punto coincide con il punto dell'estremo corrispondente. Per rispondere a una domanda del genere, si dovrebbero confrontare i valori della funzione nei punti estremi con i suoi valori alle estremità del segmento. (In pratica, per risolvere questo problema, non è necessario determinare il tipo di estremo; è sufficiente calcolare i valori della funzione nei punti critici e agli estremi del segmento e confrontarli tra loro.)

Nel 2020, questo compito ha il numero 12.

Problemi di trovare i punti estremi di una funzione.

Algoritmo per la ricerca dei punti estremi.

1) Trova il dominio della funzione.
2) Trova la sua derivata F "(X).
3) Trova i punti in cui F "(X) non esiste.
4) Trova i punti in cui F "(X) = 0.
5) Segnare sulla retta numerica il dominio di definizione della funzione e tutti i punti individuati nei commi 3 e 4. Il risultato sono gli intervalli del dominio di definizione, sui quali la derivata mantiene un segno costante.
6) Determinare il segno F "(X) per ogni intervallo. (Questo è più spesso fatto sostituendo un valore "convenienza" X da questo intervallo nella formula per la derivata ottenuta nella Sezione 2.)
7) Determinare le aree di aumento e diminuzione della funzione dai segni della derivata e trarre conclusioni sulla presenza o assenza di un estremo e sulla sua natura in ciascuno dei punti critici.

Problema 1

sì = (X+ 7) e 7 − X .

1) La funzione è il prodotto di funzioni lineari ed esponenziali, che sono definite sull'intero asse reale.
D(F) = (−∞;∞).

2) Calcoliamo la derivata, utilizzando la regola di derivazione del prodotto e le formule per la derivata della potenza e delle funzioni esponenziali.
sì" = ((X+ 7) e 7 − X)" =
= (X+ 7) "· e 7 − X + (X+ 7) ( e 7 − X)" =
= (1 + 0) e 7 − X + (X+ 7) e 7 − X(7 - X)" =
= e 7 − X + (X+ 7) e 7 - X(0 - 1) =
= e 7 − X − (X+ 7) e 7 − X .
Il calcolo della derivata è completo, ma per facilitare le azioni nei paragrafi seguenti, vale la pena convertirlo nella forma più compatta.
e 7 − X − (X+ 7) e 7 − X = e 7 − X(1 - X − 7) = −e 7 − X ·( X + 6).
Così, sì " = −e 7 − X ·( X + 6) .

3) Espressione - e 7 − X ·( X+ 6) è definito in tutti i punti dell'asse reale.
Punti dove sì" non esiste, no.

4) Risolvi l'equazione
−e 7 − X ·( X + 6) = 0.
e 7 − X 0 per qualsiasi valore X,
(X+ 6) = 0 per X = −6.

5) Rappresentiamo l'asse numerico "infinito", che nel nostro caso coincide con il dominio della funzione. Segniamo su di esso l'unico punto critico trovato X = −6.

6) Determinare i segni della derivata sulle due sezioni dell'asse risultanti.
Per x x = −10, abbiamo
sì" = −e 7 − X ·( X + 6) = −e 7 + 10 (−10 + 6) = - e 17 (−4) = 4 e 17≈4 2,7 17>0.
Per x> −6, ad esempio, per X= 7, abbiamo
sì" = −e 7 − X ·( X + 6) = −e 7 - 7 (7 + 6) = - e 0 13 = −1 13 = −13 Segna sull'asse con il segno "+" l'area dove sì"> 0 e segno "-", dove sì"

7) Nelle aree dove la derivata è positiva, la funzione aumenta, e dove la derivata è negativa, la funzione diminuisce. Mettiamo le frecce corrispondenti nella figura. Le frecce mostrano che nel punto X= −6, la funzione passa da crescente a decrescente, il che significa che questo è il punto di massimo desiderato.

Risposta: −6

Ora prova la tua forza. Per prima cosa, prova a risolvere il problema da solo, quindi confronta la risposta, quindi puoi rivelare la mia soluzione. Se la tua soluzione non è uguale alla mia, non è necessariamente sbagliata.

Attenzione: Per migliorare l'effetto didattico risposte e soluzioni vengono caricati separatamente per ogni attività premendo in sequenza i pulsanti su sfondo giallo. (Quando ci sono molte attività, i pulsanti potrebbero apparire con un ritardo. Se i pulsanti non sono affatto visibili, controlla se il tuo browser è consentito JavaScript.)

Compito 2

sì = 4X- ln ( X + 11) + 12.

Per la definizione del logaritmo X+ 11> 0, quindi D(F) = (−11;+∞).

sì" = 4 − 1 ______ X + 11 = ______ 4X + 43 X + 11 .

derivato X≠ −11, ma questo valore è al di fuori dell'ambito della funzione, quindi non è un punto critico.

sì"= 0 per 4 X + 43 = 0; X = −10,75.

sì"(−10,9) = −0,6/0,1 = −6 sì"(−10) = 3/1 = 3 > 0;

Quindi, X= −10,75 è il punto di minimo della funzione.

Risposta: −10,75

Problema 3

Trova il punto massimo della funzione sì = √16 − 4X − X 2 ___________ .

Per la definizione della radice aritmetica 16 - 4 X − X 2 ≥ 0. Per ora, non risolveremo completamente questa disuguaglianza. Nota solo che questa è una disuguaglianza quadrata e che i rami della corrispondente parabola sono diretti verso il basso. Si può concludere che un trinomio quadrato avrà valori non negativi nell'area tra le sue radici. D(F) = [X 1 ; X 2 ].

sì" = 1 ____________ 2√16 − 4X − X 2 __________ (16 - 4 X − X 2)" = − X + 2 ___________ √16 − 4X − X 2 __________ .

sì" non esiste nei punti in cui il denominatore della frazione è zero, cioè
alle 16 - 4 X − X 2 = 0. Abbiamo già designato questi punti X 1 e X 2. Sono i bordi dell'ambito della funzione.

sì"= 0 per X + 2 = 0, X = −2.

Scegliere i valori X verificare i segni della derivata sulle due sezioni risultanti. Sia -3 e 0. Assicuriamoci di non aver superato il dominio della definizione della funzione, ad es. il fatto che per questi punti è soddisfatta la disuguaglianza per l'espressione radicale. (Se completassimo immediatamente la disuguaglianza fino alla fine, non sarebbe necessario farlo. I punti verrebbero scelti in base alla figura.)
16 − 4X − X 2 ≥ 0.
16 - 4 (−3) - (−3) 2 = 19 ≥ 0.
16 - 4 0 - 0 2 = 16 ≥ 0.
Determinare i segni della derivata in questi punti

sì"(X) = − X + 2 ___________ √16 − 4X − X 2 __________ .

sì"(−3) = − −3 + 2 _____ √19 __ = 1 ___ √19 __ > 0.

sì"(0) = − 0 + 2 ____ √16 __ = − 2 _ 4 = −0,5

Quindi, X

Risposta: −2

Commento: Alcuni potrebbero trovare più facile risolvere subito l'equazione quadratica e disegnare esplicitamente il disegno finale. Fai questo.
In questo caso X 1 = −2 − 2√5_ ≈ −6,5; X 2 = −2 + 2√5_ ≈ 2,5.

Problema 4

Trova il punto di minimo della funzione sì = (0,5 − X) così X+ peccato X, appartenente all'intervallo (0, π / 2).

D(F) = (−∞;∞).

sì" = (0,5 − X) "· Cos X + (0,5 − X) (Cos X) "+ (peccato X)" =
= −cos X − (0,5 − X) peccato X+ cos X = (X- 0.5) peccato X

Punti dove sì" non esiste, no.

Risolvere l'equazione sì" = 0.
(X- 0.5) peccato X= 0 nei casi in cui
o ( X − 0,5) = 0, X = 0,5;
o peccato X = 0, X n = n.

Verifica dell'appartenenza dei valori trovati X un dato intervallo.
I valori multipli di non appartengono all'intervallo. Per n = 0, X 0 = 0, ma la spaziatura data è un intervallo e 0 non è incluso in esso. Altri valori sono maggiori di π / 2 o meno di 0.
0/2 ≈ 1,57. Punto X= 0,5 è compreso nell'intervallo specificato ed è il punto estremo. Lei è l'unica candidata per una risposta. Tuttavia, dovresti assicurarti che questo sia esattamente il minimo della funzione. Per controllare i segni della derivata nel quartiere X= 0,5 prendiamo, ad esempio, X= 0,45 e X = 0,55 .
sì"(0,45) = (0,45 - 0,5) sin0,45 = −0,05sin0,45 sì"(0,45) = (0,55 - 0,5) sin0,55 = 0,05sin0,55> 0
Quindi, a sinistra del punto 0.5, la funzione diminuisce e a destra aumenta. Il punto è il punto di minimo.

Risposta: 0,5

Commento: sin0.45 e sin0.55 sono positivi perché l'intervallo indagato corrisponde al primo quarto del cerchio trigonometrico.

Problemi di trovare gli estremi di una funzione.

1) Trova i punti estremi della funzione e determina il loro carattere allo stesso modo dei problemi precedenti.
2) Determinare i valori della funzione nei punti di massimo o minimo in base alla domanda del problema.
3) Se ci sono diversi punti di massimo (minimo) sul dominio della funzione, allora i massimi (minimi) sono chiamati locali e il più grande (il più piccolo) è chiamato il massimo globale (minimo) o il valore più grande (il più piccolo) di la funzione. Ancora una volta, leggi la domanda del problema e seleziona quella di cui hai bisogno.

Problema 5

sì = √5 − 4X − X 2 _________ .

La prima parte della soluzione coincide completamente con la soluzione del Problema 3.

5 − 4X − X 2 ≥ 0. D(F) = [X 1 ; X 2]. Qui X 1 = −5; X 2 = 1.

sì" = − X + 2 ___________ √5 − 4X − X 2 __________ .

sì" non esiste nei punti -5 e 1.

sì"= 0 per X + 2 = 0, X = −2.

sì"(−3) = 1 __ √8_ > 0; sì"(0) = − 2 __ √5_

Quindi, X= −2 è il punto massimo della funzione.

Determinare il valore della funzione a questo punto
sì(X) = √5 − 4X − X 2 __________
sì(−2) = √5 - 4 (−2) - (−2) 2 _______________ = √9_ = 3.
Le frecce in figura mostrano che il massimo nell'intero dominio della funzione è unico, quindi il valore ottenuto y (−2) = 3 sarà il valore più grande della funzione.

Risposta: 3

Problema 6

Trova il valore della funzione più piccolo sì= registro 3 ( X 2 − 6X + 10) + 2.

Per la definizione del logaritmo X 2 − 6X+ 10> 0. Il discriminante di questo trinomio quadrato D= 36 - 40 coefficiente a X 2 è uguale a 1> 0, quindi tutti i suoi valori sono positivi. Ambito della funzione D(F) = (−∞;+∞).

sì" = 1 ______________ (X 2 − 6X+ 10) ln3·( X 2 − 6X + 10)"+ 0 = ______________ 2X − 6 (X 2 − 6X+ 10) ln3.

Il denominatore di questa frazione > 0 (ln3> 1, poiché 3> e ≈ 2.7), quindi i punti in cui sì" non esiste, no.

y "= 0 se 2 X − 6 = 0; X = 3.

Il punto estremo trovato è l'unico sul dominio di definizione della funzione; lo divide in due sezioni, e per X x> 3 y "> 0, il che significa che questo è il punto del minimo globale.

Trova il valore della funzione a questo punto
sì(3) = registro 3 ( X 2 − 6X+ 10) + 2 = log 3 (3 2 - 6 3 + 10) + 2 = log 3 1 + 2 = 0 + 2 = 2.
Questo è il valore più piccolo della funzione sull'intero dominio.

Risposta: 2

Compiti per determinare il valore più grande (più piccolo) di una funzione su un segmento.

Funzione continua su un segmento raggiunge i suoi valori più piccoli e più grandi sia nei punti interni dell'intervallo, sia alle sue estremità. Pertanto, per risolvere i problemi di questa sezione, è sufficiente determinare i valori della funzione nei punti estremi e confrontarli con i suoi valori alle estremità del segmento. Non è necessario identificare il tipo di estremo.

Se almeno una delle due condizioni non è soddisfatta - la funzione risulta discontinua o viene specificato un intervallo (semi-intervallo) come intervallo, sarà necessaria un'analisi completa del comportamento della funzione e della sua derivata , e non il fatto che la risposta esisterà. All'esame non sono ancora stati riscontrati problemi con condizioni così complicate, e chi è semplicemente interessato può seguire il link e

Problema 7

Trova il valore della funzione più grande sì = X 3 + 2X 2 + X + 3 sul segmento [−4; −1].

D(F) = (−∞;+∞).
sì" = 3X 2 + 4X + 1.
La funzione è continua in tutto il dominio.
Punti dove sì" non esiste, no.
Risolvere l'equazione sì" = 0: 3X 2 + 4X + 1 = 0
Discriminante D= 16 - 12 = 4. Radici X 1,2 = −4 ± 2 ______ 6, X 1 = −1/3; X 2 = −1.

Trova i valori della funzione in questi punti e ai bordi del segmento
sì(X) = X 3 + 2X 2 + X + 3;
sì(−4) = (−4) 3 + 2 (−4) 2 - 4 + 3 = −64 + 2 16 - 4 + 3 = −33;
sì(−1/3) = (−1/3) 3 + 2 (−1/3) 2 - 1/3 + 3 = −1/27 + 2 1/9 −1/3 + 3 = 2 23 __ 27 ;
sì(−1) = (−1) 3 + 2 (−1) 2 - 1 + 3 = −1 + 2 - 1 + 3 = 3.

Scegliendo il più grande dei valori risultanti sì... esso sì(−1) = 3.

Risposta: 3

Problema 8

Trova il valore della funzione più grande sì= 36tg X − 36X+ 9π + 7 sul segmento [−π / 4; / 4].

Sul segmento [−π / 4; π / 4], la funzione data è definita e continua (vedi grafico tg X).

sì"= 36 _____ 1 cos 2 X − 36 + 0;

sì" non esiste per cos X = 0, X n = _ π 2· N, n Є Z. Nessuno di questi punti è compreso nell'intervallo [−π / 4; / 4].

sì"= 0 a cos 2 X= 1, cos X= ± 1, X k = πk, k Є Z. Il segmento [−π / 4; π / 4] solo il punto appartiene X 0 = 0.

Determina i valori della funzione in questo punto e alle estremità del segmento.
sì(X) = 36tg X − 36X+ 9π + 7
sì(0) = 36tg0 - 36 0 + 9π + 7 = 0 - 0 + 9π + 7 ≈ 9 3,14 + 7 = 35,26
sì(−π / 4) = 36tg (−π / 4) - 36 (−π / 4) + 9π + 7 = 36 (−1) + 9π + 9π + 7 = −29 + 18π ≈ −29 + 18 3,14 = 27.52
sì(π / 4) = 36tg (π / 4) - 36 / 4 + 9π + 7 = 36 1 - 9π + 9π + 7 = 43.
Il più grande di questi numeri è 43.

Risposta: 43

Commento: Nel differenziare, ricorda che è la stessa costante di qualsiasi altro numero. Quindi "= 0.

Problema 9

Trova il valore della funzione più grande sì = 2X 2 − 13X+ 9ln X + 8 sul segmento [ 13 __ 14 ; 15 __ 14 ] .

La funzione è definita e continua per tutti X> 0, compreso sul segmento [ 13 __ 14 ; 15 __ 14 ].

sì" = 4X- 13 + 9 1 _ X + 0 = 4X 2 − 13X + 9 ___________ X

sì" non esiste per X= 0. Questo punto non è incluso nell'intervallo specificato. Non lo consideriamo.

sì"= 0 per 4 X 2 − 13X + 9 = 0
Risolviamo questa equazione quadratica attraverso il discriminante, troviamo le radici X 1 = 1, X 2 = 9/4 = 2,25.

X 1 = 1 è il punto medio di un dato segmento, X 2 = 2.25 non appartiene al segmento. Quindi è necessario determinare i valori della funzione y (13/14), y (1) e y (15/14) e confrontarli tra loro. Tuttavia, in questo caso, il calcolo dei valori di y (13/14) e y (15/14) potrebbe essere troppo complicato e molto probabilmente portare a errori. È più facile tornare allo studio del comportamento della derivata in prossimità del punto estremo trovato.

sì"è una frazione il cui denominatore è positivo sul segmento. Ciò significa che il segno della derivata su questo segmento dipende solo dal numeratore, cioè determinato dal segno del trinomio quadrato 4 X 2 − 13X + 9. Il grafico di questo trinomio quadrato è una parabola con rami rivolti verso l'alto (4> 0), che incrociano l'asse delle ascisse in due punti X 1 e X 2. Disegniamo "a mano" uno schizzo di questo grafico e vediamo quello a sinistra della radice X 1 trinomio quadrato, il che significa che l'intera derivata avrà un segno "+" e a destra - un segno "-".
Conclusione: la funzione specificata nella dichiarazione del problema su un dato segmento a sinistra X 1 = 1 aumenta, a destra - diminuisce. Questo punto è il punto massimo all'interno del segmento, il valore della funzione in esso sarà il più grande.